SUMMARY
The discussion centers on the relationship between the angle of a slope and the acceleration of a solid sphere rolling down it. The acceleration formula derived is \( a = \frac{5}{7}g\sin{\theta} \), with the derivative \( \frac{da}{d\theta} = \frac{5}{7}g\cos{\theta} \) indicating that as the angle \( \theta \) approaches \( 90^\circ \), the gradient of acceleration decreases, leading to diminishing returns in acceleration for equal increments in angle. The conversation also touches on the effects of friction and air resistance, though these factors primarily alter the leading coefficient rather than the fundamental relationship between acceleration and angle.
PREREQUISITES
- Understanding of basic calculus, particularly derivatives
- Familiarity with trigonometric functions, specifically sine and cosine
- Knowledge of Newtonian mechanics, particularly the motion of objects on inclined planes
- Basic understanding of forces acting on a solid sphere, including gravity and friction
NEXT STEPS
- Study the derivation of the acceleration formula for objects on inclined planes
- Learn about the effects of friction on rolling motion, particularly for solid spheres
- Explore the relationship between angle and acceleration in more complex systems, such as V-shaped tracks
- Investigate the role of air resistance in the motion of rolling objects
USEFUL FOR
Physics students, educators, and anyone interested in the dynamics of rolling motion on inclined planes will benefit from this discussion. It provides insights into the mathematical relationships governing acceleration and angle, as well as practical implications for real-world applications.
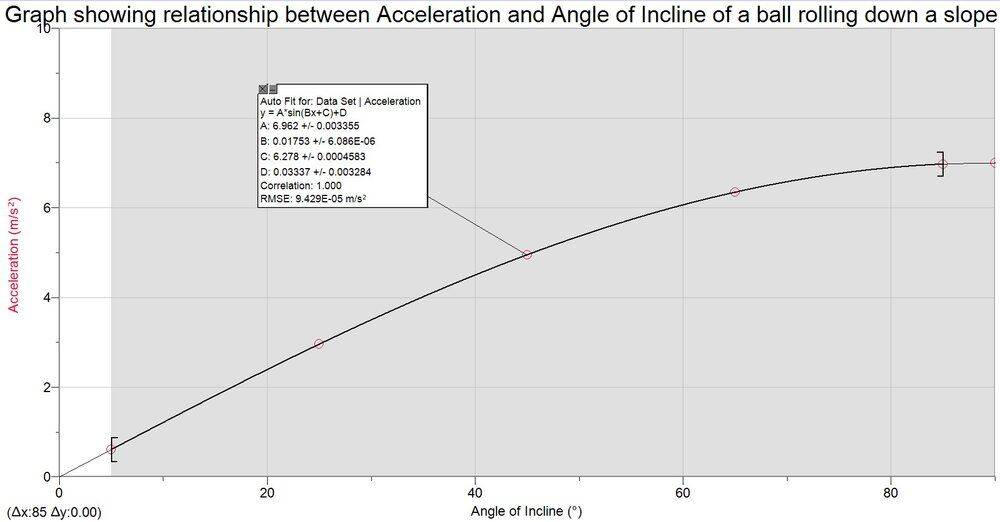
 . The ##5/7## is correct for the flat ramp. Just ignore me
. The ##5/7## is correct for the flat ramp. Just ignore me