Why Does arccos(x) - arcsin(1-x) Equal 90° Have No Solutions?

[acen_gr]

Did you just do what I think you did?

To quote myself from earlier:

Oopps. My bad. But I will work on it again. I'm sure my answer would still be the same. I'm going to repost it to make it clear :shy:

 

[Mentallic]

Oopps. My bad. But I will work on it again. I'm sure my answer would still be the same. I'm going to repost it to make it clear :shy:

If you do it correctly, your answer should be way more nonsensical than x=0 is

 

[acen_gr]

arccos(x) - arcsin(1-x) = 90°

arccos(x) = 90° + arcsin(1-x)

taking cosine of both sides:
x = cos[90° + arcsin(1-x)]
x = cos90°cos[arcsin(1-x)] - sin90°sin[arcsin(1-x)]
x = -sin[arcsin(1-x)]
x = -(1-x)
x = -1 + x
0 = -1
^ again, makes no sense

 

[Mentallic]

0 = -1
^ [STRIKE]again[/STRIKE], makes no sense

Fixed. There was never a first time that you proved that it makes no sense hehe

 

[acen_gr]

No way! 2x=0 implies that x=0. Of course this makes sense!

Such things that would be nonsense would be if we divided by 0, or if we tried to take the square root of a negative, or the arcsin of a value outside the range -pi/2 to pi/2, or something like 1=0.

Yeah and I think I should work on remembering things
There really is a sense in 2x = 0 (how could I say it doesn't :shy:)

Since my proof that time is senseless (because I did the wrong way of taking cosine of both sides), this x = 0 doesn't happen to be a solution right? Because what I was trying to prove is that solution is nowhere to find.

 

[acen_gr]

Fixed. There was never a first time that you proved that it makes no sense hehe

I was about to say that I'm referring to this:

I'm sure my answer would still be the same.

**Just wants escape the truth**

 

[Mentallic]

Since my proof that time is senseless (because I did the wrong way of taking cosine of both sides), this x = 0 doesn't happen to be a solution right? Because what I was trying to prove is that solution is nowhere to find.

Say I want to find the solution to x such that it satisfies x+2=0, so I go about it by dividing through by 2 (incorrectly) and get x+1=0, so x=-1. Is x=-1 a solution to x+2=0?

Since you made an error in your calculations, of course the answer isn't going to correct!

Haha just don't let me catch you taking the cosine of a sum in the wrong way again

 

[acen_gr]

Say I want to find the solution to x such that it satisfies x+2=0, so I go about it by dividing through by 2 (incorrectly) and get x+1=0, so x=-1. Is x=-1 a solution to x+2=0?

Since you made an error in your calculations, of course the answer isn't going to correct

Now that's clear. I second thought because my answer in the wrong proof and right proof says the same. Now I had this conclusion that doing cosine incorrectly sometimes gives some right answers

Haha just don't let me catch you taking the cosine of a sum in the wrong way again

Aye aye captain! I just loved algebra that much than trigonometry. So I tend to use it on trigonometry. LOL

 

[acen_gr]

To forum moderators/admins, you may lock this thread now to avoid spamming. I believe it already served its purpose. Just hoping that it won't get immediately deleted due to some reason. If this thread in any way violated the rules, please inform before deleting so I can work on it. Some may find this thread useful to answer their questions. Thank you.

Also, many thanks to mentors Simon Bridge, micromass, Mentallic and https://www.physicsforums.com/member.php?u=147785 for contributing answers to this question.

 

[Simon Bridge]

(1) The post is not misstated.

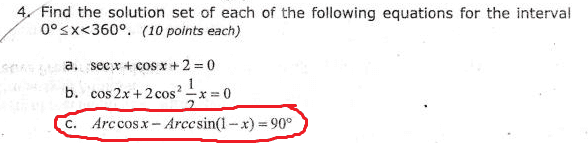
(c) is the odd one out isn't it?

the given range for x is fine for the 1st two but not for (c)
"arcsin" is misspelled as arccsin.
what other carelessness is there?

ask your teacher for a model answer - showing working.

UPDATE: Anyway sir, how do you find out the solution of trigonometric equations through graphs? Like the one you posted in post #27.

I used gnu-octave to plot the graph ... the solution would have been the intersection of the curve with the line y=90.

The code was:

> x=0:0.0125:1;
... says to make a vector whose first entry is 0, incrementing by 1/80 until it reaches 1;

> y=acos(x)-asin(1-x);
... this is the function I want to plot a graph of: y will be in radiens;
... the result of y will be a vector the same size as x, each entry being the result of plugging the corresponding x entry into the equation.

> plot(x,y*(180/pi))
... this plots the graph - I scales the y-axis to give degrees.
... plot(X,Y) treats the two vectors X and Y as ordered pairs (Xi, Yi).

I could have plotted a line at y=90 by doing:
> plot([0,1],[90,90])
... because the plot function automatically draws a line between data points.
... plot will interpret the two vectors as the points (0,90) and (1,90).


generally: if I want to solve f(x)=c, then I could plot y=f(x) and y=c, plot both on the same axis and note the intersection ... reading x off the horizontal axis.

That is usually good for simple relations or for an approximation. For more precision, I'd use Newton-Raphson on f(x)-c=0 - using the graph to select initial values of x.

Some ability to plot the relations you are trying to solve is invaluable: it tells you what kind of solution you are aiming for. Octave is free/libre as well as free/gratis, others use Matlab or Mathematica. Only masochists use spreadsheets for stuff like this.

I guess that is pretty much all this topic exhausted - cheers.

 

[acen_gr]

(1) The post is not misstated.

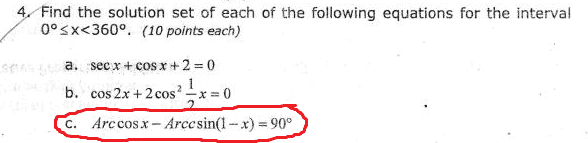
(c) is the odd one out isn't it?

the given range for x is fine for the 1st two but not for (c)
"arcsin" is misspelled as arccsin.
what other carelessness is there?

ask your teacher for a model answer - showing working.

I truly agree with you sir. That's why I rather choose to drop all my subjects and just study by myself here than to listen to him who even doesn't know what he's saying. He's making us fail in class by teaching us easy examples and giving out hard tests. Glad that I found this site where I can learn genuinely. The questions I am posting here in physics forum are all the hard questions which are not taught to us how to solve, yet still included in exams (yes, they're that harsh).

Anyway, GNU octave sounds very cool! Someday I would like to know how to use it

EDIT: Sad to say our school might not teach us that. We're late when it comes to technology *sigh*

 

[Simon Bridge]

http://www.gnu.org/software/octave/
... works on windows, osx, android and gnu/linux - the bigger linuxes provide it in their repositories.

 

[SammyS]

https://www.physicsforums.com/attachment.php?attachmentid=50336&stc=1&d=1346433295

Well, it's easy to see how the erroneous restriction of 0° ≤ x ≤ 360° got into the problem.

That restriction makes sense for (a) & (b), but not for (c), and part (c) is what this thread is about.

The domains of the arccosine and acrsine function restrict the domain of arccos(x) - arcsin(1-x) to 0 ≤ x ≤ 1 .

Using the identity

90^{\circ}-\arccos(x)=\arcsin(x)​

shows that the given equation is equivalent to

\arcsin(1-x)+\arcsin(x)=0\ .​

A graph of y = arcsin(1-x) + arcsin(x) shows that it has no zeros. (It has no x-intercept.) So the problem has no solution, as others have pointed out.

A graph of this function from WolframAlpha may be helpful.