Why Does Changing Order of Rate Adjustments Affect the Final Outcome?

  • Context: MHB 
  • Thread starter Thread starter kdan78
  • Start date Start date
Click For Summary
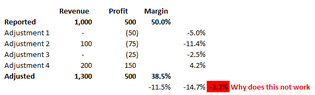
SUMMARY

The discussion centers on the mathematical principle that changing the order of rate adjustments affects the final outcome due to different bases for each calculation. Participants highlight a common example involving a 10% decrease followed by a 10% increase, illustrating that the final result does not return to the original value. The conversation emphasizes that the sequence of adjustments significantly influences the overall impact, particularly when the adjustments are not uniform. This principle is crucial for understanding financial calculations and rate adjustments.

PREREQUISITES
  • Understanding of percentage calculations
  • Familiarity with the concept of base values in mathematics
  • Knowledge of financial adjustment techniques
  • Basic algebraic manipulation skills
NEXT STEPS
  • Research the concept of "Percentage Change" in financial contexts
  • Learn about "Compound Interest" and its effects on rate adjustments
  • Explore "Order of Operations" in mathematical calculations
  • Study "Base Value Adjustments" in economic models
USEFUL FOR

Mathematicians, financial analysts, educators, and anyone involved in calculations that require precise understanding of rate adjustments and their implications.

kdan78
Messages
2
Reaction score
0
I am having a tough time figuring out why the change in the rates in this problem is not equal to the sum of the pieces, any assistance would be appreciated:

View attachment 7727
 

Attachments

  • math problem.PNG
    math problem.PNG
    3.8 KB · Views: 91
Mathematics news on Phys.org
Different Bases for each individual calculation.

It doesn't work for the same reason that the old trick question doesn't get you back where you started...

What is 100 less 10% and then the result is increased by 10%? Please respond to this question.
 
tkhunny said:
Different Bases for each individual calculation.

It doesn't work for the same reason that the old trick question doesn't get you back where you started...

What is 100 less 10% and then the result is increased by 10%? Please respond to this question.

Agree, but then the order of the adjustments would dictate the impact. Meaning the 4th adjustments will have one bases point impact as the last adjustment but a different impact as the first adjustment.

- - - Updated - - -

tkhunny said:
Different Bases for each individual calculation.

It doesn't work for the same reason that the old trick question doesn't get you back where you started...

What is 100 less 10% and then the result is increased by 10%? Please respond to this question.

99,
 

Similar threads

MHB Switch from rings and modules to analysis
  • · Replies 2 ·
Replies
2
Views
2K
MHB Using line equations to calculate a difference in rates of development
  • · Replies 1 ·
Replies
1
Views
2K
MHB HELP How to calculate wage for assistants at hair salon?
  • · Replies 2 ·
Replies
2
Views
2K
Graduate What motivates famous mathematicians?
  • · Replies 2 ·
Replies
2
Views
2K
MHB Couple of hard trig questions....
  • · Replies 1 ·
Replies
1
Views
2K
MHB Manipulating quadratic and exponential expressions
  • · Replies 1 ·
Replies
1
Views
3K
MHB Liquid Blending Proportions - Problem Setup
  • · Replies 4 ·
Replies
4
Views
3K
Undergrad Please help me understand the double slit experiment and conclusion
  • · Replies 65 ·
3
Replies
65
Views
4K
How to calculate time of Pressurization in vessel?
  • · Replies 15 ·
Replies
15
Views
5K
Why does graphene tend to break during mechanical exfoliation?
  • · Replies 2 ·
Replies
2
Views
2K