Why Does My MATLAB Code Produce Incorrect Fourier Coefficients?

[skooteryup]

Hey guys, I'm working on a MATLAB program to find Fourier coefficients.

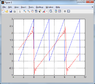
The problem with it: [STRIKE]it gives a graph that has a different period and amplitude than the original function (although its the same general shape).[/STRIKE]

[STRIKE]I've uploaded a screenshot of the graph that I'm referring to (as an attachment to this thread) so that you don't have to run the program hopefully.[/STRIKE]

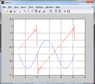
EDIT: It's just a coincidence the graphed coefficients happen to resemble the original function (sawtooth(x)). I changed y and y_test to equal sin(x) and the same coefficient graph appears. Can anybody give me a better algorithm for modeling the Fourier coefficients? I guess I've been working on this too much, I can't seem to be able to figure it out. I've also uploaded the graph.

Heres my code:

%% I_A
% BEGIN SOME FUNCTION AND VARIABLE DECLARATIONS
syms x;
length_of_k = 25;            % Number of coefficients to calculate
p = pi;                      % Function period
y = sin(x);                  % Function
x_test = -p : 1/25 : 2*p;   % Original x values
y_test = sin(x_test);        % Original f(x)
% END SOME FUNCTION

% BEGIN COMPUTING FOURIER COEFFICIENTS
% -- BEGIN NOTES --
% Calculate : a_0, a_k, b_k with k > 0
% a_0 = (1/p)*int(f(t), t, 0, p) -- Integral f(t) w.r.t. t from 0 to p
% a_k = (2/p)*int(f(t)*cos((2*pi*k*t)/p), t, 0, p)
% b_k = (2/p)*int(f(t)*sin((2*pi*k*t)/p), t, 0, p)
% -- END NOTES --

a_0 = (1/p)*int(y, x, 0, p); % Calculate as priming reed
a_coeff = [];                % Declaring null array
b_coeff = [];                % Declaring null array
fprintf('Fourier Coefficient:\ta_0 ==> %0.2f\n', double(a_0))

for k = 1 : length_of_k
    a_coeff = [a_coeff, (2/p)*int(x*cos(2*pi*k*x/p), x, 0, p)];
    b_coeff = [b_coeff, (2/p)*int(x*sin(2*pi*k*x/p), x, 0, p)];
    fprintf('Fourier Coefficient:\t');
    fprintf('a_%1.0f ==> %0.3f\t\t', k, double(a_coeff(k)));
    fprintf('b_%1.0f ==> %0.3f\n', k, double(b_coeff(k)));
end
% END COMPUTING FOURIER COEFFICIENTS

% BEGIN GENERATING FOURIER TERMS
fs_x = [];
fs_a0_calc = (a_0/2);
for i = 1 : length(x_test)
    a_calc = 0;
    b_calc = 0;
    for k = 1 : length_of_k
        a_calc = a_calc + a_coeff(k)*cos(k*x_test(i));
        b_calc = b_calc + b_coeff(k)*sin(k*x_test(i));
    end
    fs_x = [fs_x, fs_a0_calc + a_calc + b_calc];
end
% END GENERATING FOURIER TERMS

% BEGIN PLOTS
plot(x_test, y_test, 'b', x_test, fs_x, 'r');  % Plot the original function
grid on;                                       % Turn on grid
% END PLOTS

% BEGIN DEBUGGING CODE
fprintf('Max of f(x) = %0.4f\n', max(y_test));
fprintf('Min ox f(x) = %0.4f\n', min(y_test));
fprintf('Max of FS[x] = %0.4f\n', max(double(fs_x)));
fprintf('Min of FS[x] = %0.4f\n', min(double(fs_x)));
% END DEBUGGING CODE

Any help is greatly appreciated!

 

[Dr Transport]

Here is a function I wrote for a square wave...

clear all;

num_coeff = 25;

num_terms = 500;

period = pi;

x = linspace (0, 2*period, num_terms);

for i =1:num_coeff
	for j = 1:num_terms
		a(i,j)= cos(i*x(j)*pi/(period));
		b(i,j)= sin(i*x(j)*pi/(period));
	end
end 

for i = 1:num_terms
	if i <=num_terms/2
		y(i) =1;
	endif
	if i >num_terms/2
		y(i) =-1 ; 
	endif 
end

A_0 = sum(y)*(period*2/num_terms)/(2*period);
A = y*a'/(period)*(period*2/num_terms);
B = y*b'/(period)*(period*2/num_terms);


Cos_Matrix = A*a;
Sin_Matrix = B*b;

Z = A_0 + Cos_Matrix + Sin_Matrix;

plot(x, Z)