Why does Planck's BB emissive power increase with n?

[kayan]

This question is regarding the dependence of Planck's law for black-body (BB) radiation intensity (or integrating over a hemisphere, the emissive power, E = pi * I).
Physically speaking, why is it that a BB emitting in a medium with n>1 (n being index of refraction) emits a higher power/area than the same BB (same T, same everything) in a vacuum (n=1)?

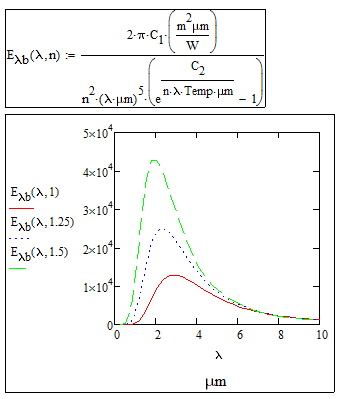
Obviously, I can just plug greater values of n into Planck's law to see this mathematically, and I have done that in the plot attached below for n values 1 (red, bottom), 1.25 (blue, mid), 1.50 (green, top). However, how can I make sense of this trend? It seems counter intuitive that if radiation has to travel through a medium with a higher n (slower speed), then the power increases? I've tried over and over to rationalize this trend using both photon and wave behavior, but cannot come to a rationale that makes sense. For example, in the photon perspective, higher n means each photon travels slower in the medium, which means that the spatial photon intensity increases, however, since the photons are traveling slower, this also means that whatever object they are irradiating, they would take longer to reach that object (even though they are closer together spacially), hence, there wouldn't be a change.

 

[mfb]

You can get an intuition from an equilibrium in a volume partially filled with a medium with n>1 and vacuum, for example. All light from the vacuum will enter the medium (and get a bit collimated), but in the medium some light will get reflected back at the surface and only light under some angle can go to the vacuum. The medium has conditions that act like a larger than 4 pi solid angle.

 

[kayan]

Not sure if that makes sense to me. First of all, can you describe the geometry a little better (spherical, a wall, etc)? Second of all, you mentioned "reflection", however, Planck's law doesn't say anything about reflection. It is only describing the power intensity radiating from a BB. If there is reflection or other modes of transmission going on, those are independent and secondary effects, and effects that should not have any bearing on how the value of n affects Planck's law.

 

[mfb]

First of all, can you describe the geometry a little better (spherical, a wall, etc)?

It does not matter, as long as there is a surface between the materials of different refractive index.

however, Planck's law doesn't say anything about reflection.

Planck's law says something about an equilibrium condition. It is possible to analyze the same thermal equilibrium conditions elsewhere.

 

[kayan]

Let's talk about specifics. Say there is a BB sphere in a vacuum, and then there is a medium with n>1 after light passes through the vacuum. So you're saying that the reason the emissive radiation increases is because the radiation emits from the BB, travels through the vacuum, then some of it gets reflected at the medium interface, goes back to the BB, and gets absorbed more which increases its temperature and hence the radiation it then emits?

 

[mfb]

Let's talk about specifics. Say there is a BB sphere in a vacuum, and then there is a medium with n>1 after light passes through the vacuum.

In this case the power does not increase, but this is neither the thermal equilibrium case I was considering nor the direct emission into a medium as in your initial question.

 

[kayan]

Does anybody else have an explanation? Still haven't heard an answer that makes sense to me.

 

[jartsa]

An antenna might be too short to radiate long waves efficiently. But if we immerse that antenna in a liquid where speed of light is low, the antenna works better, at low frequencies. Then we might say: "radiation resistance increased".

A black body consists of antennas that are mostly microscopic, that's why its radiation power at low frequencies is low.

Why do cold black bodies radiate best at low frequencies?

 

[Charles Link]

Does anybody else have an explanation? Still haven't heard an answer that makes sense to me.

I have one possibility that could explain the formulas that you have. I would normally like to see the geometric conditions upon which these formulas were derived to try to validate/verify them, but taking them as likely to be accurate, perhaps one explanation for a higher emission rate is the critical angle that exists for total internal reflections that may affect the total integrated result. The specifics for which your formulas might apply have not been detailed, but I'm just giving one possibility that might account for some differences.

 

[jartsa]

If we consider a closed box of graphite walls at a constant temperature with a small hole on one side and some material with high refractive index covering the hole, we can see that the quantum-waves, or waves of probability of detecting a radiation photon, propagate slowly in the material, which causes the wave-crests near the hole to turn towards the hole.

And that causes some 'extra' photons to be detected in the material, and some photons 'missing' in the box.

In other words the material with high refractive index sucks radiation from the box.