mangoplant
- 5
- 0
Here is an interesting phenomenon: If one were to drill a hole that went all the way to the center of the Earth and drop an object through the hole, according to a model called PREM (Preliminary Reference Earth Model), the acceleration of the object would initially increase as it approached the outer core of the Earth and then decrease as the gravitational pull from the mass above the object started canceling the gravitational pull from the mass below (see pic below).
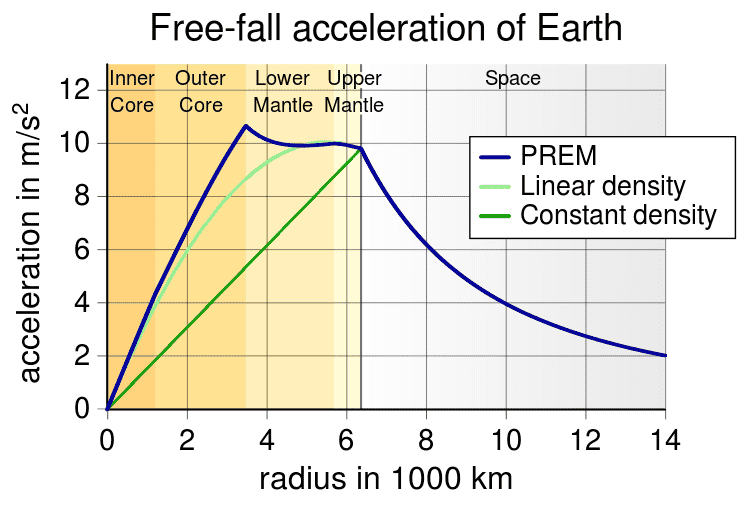
Now Newton's law of gravitation predicts that the acceleration should decrease as an object moves down the hole because there is less mass below the object and more above, pulling in the other direction. Anyone know why this widely accepted PREM model predicts otherwise?Here is Newton's law of gravitation prediction where
 is the mass of the object,
is the mass of the object,
 is the distance from the core,
is the distance from the core,
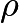 is the density of the Earth (assuming it is constant),
is the density of the Earth (assuming it is constant),
 is the gravitational constant, and
is the gravitational constant, and
 is the acceleration of the object.
is the acceleration of the object.
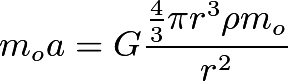
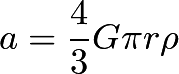
Clearly, Newton's law predicts something very different from the PREM model.
How could acceleration possibly increase according to the PREM model when there is less mass below the object as it is moving toward the core?
Now Newton's law of gravitation predicts that the acceleration should decrease as an object moves down the hole because there is less mass below the object and more above, pulling in the other direction. Anyone know why this widely accepted PREM model predicts otherwise?Here is Newton's law of gravitation prediction where
Clearly, Newton's law predicts something very different from the PREM model.
How could acceleration possibly increase according to the PREM model when there is less mass below the object as it is moving toward the core?