of course. But i think you are not quite completely thinking through what happens to torque as the motor starts.
Torque developed by the motor doesn't all go into driving an external mechanical load, much of it must go into
accelerating the motor plus its external load. So what you measure at the shaft must be corrected for dω/dt and total moment of inertia.
Have you ever listened while a motor starts a high inertia load like a bench grinder with two big heavy wheels??
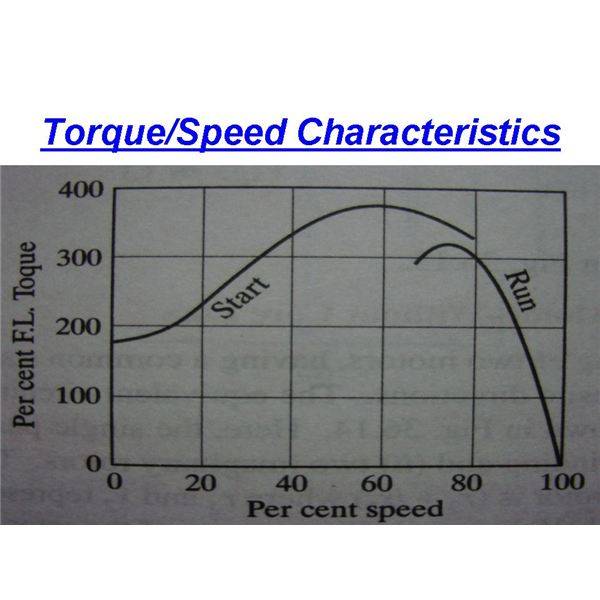
You'll hear it hum and accelerate slowly until speed approaches that peak region
then speed almost
snaps up that last few hundred RPM to near synchronous.
That to me is the a beautiful demonstration of the effect Mr Av'supernova described. Surely a friend has an old fashioned bench grinder where you could experiment. Grind on something and feel how steep is the Right-hand slope of that speed/torque curve. Then force it past peak and feel how easily you can
grindoohh terrible pun-sorry it to a halt.
in most motors torque increases until peak, decreases thereafter because of ratio of rotor resistance to inductance.
Remember a lot of torque goes into accelerating the rotating inertia
so to measure it you'd have to use a brake and hold speed constant at each data point.
Designers can build the rotor to give custom speed-torque curves by adjusting size & shape shape of rotor bars to tweak their resistance and moving them deeper into the iron to tweak their inductance.
you'd want an A curve motor for a bench grinder because it'd really hang in there when you get aggressive on a workpiece
and a D curve for an elevator because its curve has no cusp - only sudden change of acceleration will be at start and stop giving a perceived smoother ride.. no'jerk'
this is a nice page to peruse, that 'typical' curve set just above came from it.
http://ecmweb.com/motors/understanding-induction-motor-nameplate-information
in my motors class (1965) we had an induction motor with wound rotor and brushes. That let us use an external rotor resistor so we could run it any class, and did such experiments. I hope such labs still exist for undergrads. I visited my Alma Mater a couple months ago, walking through that lab was nostalgic but my goodness how the electronics has taken over motor drives!
old jim