- #1
22990atinesh
- 143
- 1
Why Graphing Tools doesn't represent hole in a graph of a function. A Hole at a point in a graph is point where function is not defined.Suppose there is a function
##\frac{x}{\root{x-1}-1}##
Its should be like this
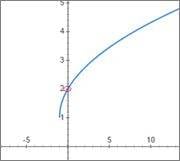
But online tools and even my android graphing tool app shows graph like this
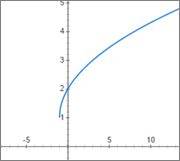
What I'm saying is that, apart from circle there must be some sort of marks representing that the function is not defined here.
##\frac{x}{\root{x-1}-1}##
Its should be like this
But online tools and even my android graphing tool app shows graph like this
What I'm saying is that, apart from circle there must be some sort of marks representing that the function is not defined here.