SUMMARY
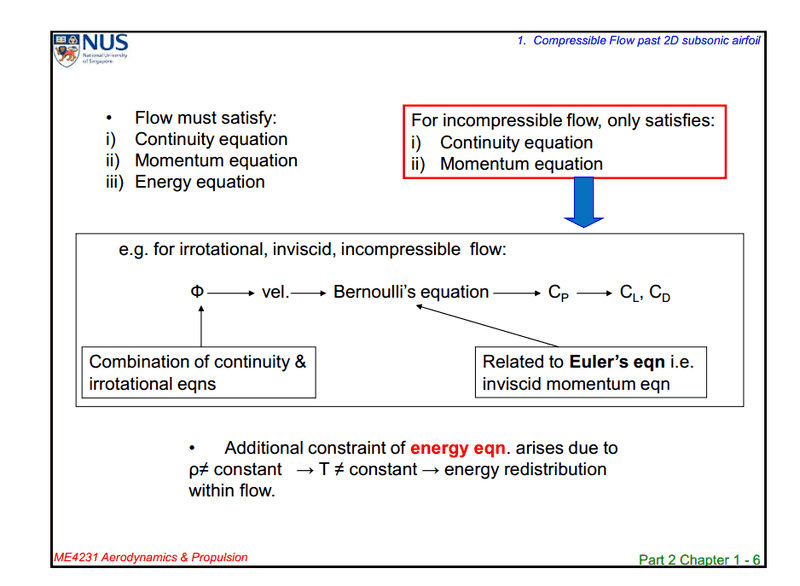
The discussion clarifies that incompressible flow does satisfy the energy equation, contrary to some misconceptions. While incompressible flows can decouple the energy equation from mass and momentum conservation equations, they can still be relevant under conditions of significant viscous heating or external heat transfer. The conversation also highlights the existence of three flow regimes: incompressible, variable-density, and compressible, with variable-density flows being a nuanced category that may still exhibit incompressibility in certain contexts. The participants emphasize the importance of understanding these distinctions in fluid dynamics.
PREREQUISITES
- Understanding of fluid dynamics principles
- Familiarity with the continuity and momentum equations
- Knowledge of energy balance equations in fluid mechanics
- Concept of variable-density flows versus incompressible flows
NEXT STEPS
- Research the implications of viscous heating on incompressible flow
- Study the characteristics of variable-density flows in fluid dynamics
- Explore the relationship between temperature variations and viscosity in fluids
- Investigate the distinctions between subsonic and supersonic compressible flows
USEFUL FOR
Fluid dynamics students, mechanical engineers, and researchers focusing on flow regimes and energy equations in incompressible and compressible fluids.