Modeling ideal gas flow using Bernoulli's equation

[MexChemE]

Hello, PF!

I'm currently brushing up my fluid mechanics and came across some questions while studying the compressible flow of an ideal gas using Bernoulli's equation. First, consider incompressible flow in the following system

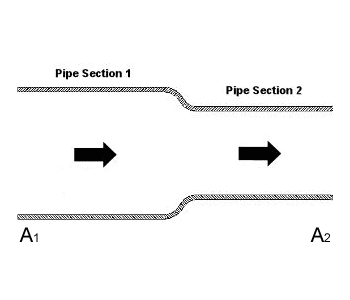
Neglecting any changes in elevation, the Bernoulli equation for this system is
P_1 - P_2 = \frac{1}{2} \rho \left( v_2^2 - v_1^2 \right)
And the continuity equation states
A_1 v_1 = A_2 v_2
Now, since A_1 > A_2, then v_2 > v_1, therefore P_1 > P_2. An increase in velocity results in a decrease in pressure. This is Bernoulli's principle.

Now consider the isothermal flow of an ideal gas through the same system. Bernoulli's equation in this situation is
\frac{RT}{M} \ln{\frac{P_1}{P_2}} = \frac{1}{2} \left( v_2^2 - v_1^2 \right)
I'm going to call this equation A. This equation has units of energy per unit mass. Now, the continuity equation for this case is
\rho_1 A_1 v_1 = \rho_2 A_2 v_2
Or, using the ideal gas law
P_1 A_1 v_1 = P_2 A_2 v_2
Now, according to equation A, if v_2 > v_1, then P_1 > P_2, so Bernoulli's principle holds. However, this is where I'm having a little bit of trouble, in the incompressible case, the decrease in flow area is what caused the increase in velocity (and will always do, according to the continuity equation). In the compressible case (and again, according to the corresponding continuity equation) a decrease in flow area may not always result in an increase in velocity, since we have to take into account the change in density/pressure of the gas. In other words, for this particular system, even if A_1 > A_2 will always be true, v_1 may be greater or smaller than v_2, depending on the nature of the gas and the temperature of the system. Is this right?

Are there any rules of thumb or other relationships between flow area and velocity for compressible flows? I know this might seem like a simple detail but it really caught me off guard.

Also, for the incompressible case, is it okay to use gauge pressures in calculations involving the Bernoulli equation or any other form of the mechanical energy balance?

Thanks in advance for any input!

 

[Chestermiller]

Why don't you write the equation as \ln{\frac{P_1}{P_2}} = \beta \left[ \left( \frac{v_2} { v_1}\right)^2-1 \right]
where $\beta$ is the (positive) dimensionless group $\frac{Mv_1^2}{2RT}$? Then substitute this into the equation P_1 A_1 v_1 = P_2 A_2 v_2 and solve for $A_2/A_1$ as a function of $v_2/v_1$. Then plot a graph of $A_2/A_1$ vs $v_2/v_1$ with $\beta$ as a parameter and see what you get.

For the incompressible case, it is always okay to use gauge pressures.

 

[MexChemE]

Why don't you write the equation as \ln{\frac{P_1}{P_2}} = \beta \left[ \left( \frac{v_2} { v_1}\right)^2-1 \right]
where $\beta$ is the (positive) dimensionless group $\frac{Mv_1^2}{2RT}$? Then substitute this into the equation P_1 A_1 v_1 = P_2 A_2 v_2 and solve for $A_2/A_1$ as a function of $v_2/v_1$. Then plot a graph of $A_2/A_1$ vs $v_2/v_1$ with $\beta$ as a parameter and see what you get.

For the incompressible case, it is always okay to use gauge pressures.

Sweet, that looks promising, I'll come back once I get these results. Is the \beta parameter commonly encountered in compressible flow situations? Does it have a range of "typical" values? It looks like the ratio between the gas' kinetic and internal (?) energies.

One more question, though, is the pressure term in the Bernoulli equation what we would normally read in an actual pressure gauge? I've always had that doubt and never got the chance to clear it out.

 

[Chestermiller]

Sweet, that looks promising, I'll come back once I get these results. Is the \beta parameter commonly encountered in compressible flow situations? Does it have a range of "typical" values? It looks like the ratio between the gas' kinetic and internal (?) energies.

I've never seen this group before. It just seems to emerge naturally from the equation. To get typical values, just substitute some situations. Play with it.

One more question, though, is the pressure term in the Bernoulli equation what we would normally read in an actual pressure gauge? I've always had that doubt and never got the chance to clear it out.

If the gauge opening is oriented parallel to the flow, then it measures the static pressure. If it is oriented perpendicular to the flow, then it measures the total pressure (static plus dynamic).

 

[MexChemE]

Okay, here it is.

The system I described has the condition \frac{A_2}{A_1} < 1, so in order for the gas to flow from point 1 to point 2, it must operate at low \beta values. If it operated at higher \beta values the gas would flow from 2 to 1 (v_1 > v_2). One thing that's confusing me is that when v_1 = v_2, A_1 = A_2 and P_1 = P_2, where this last equality means there is no flow, and I'm pretty sure compressible flow of a gas in a constant area channel exists. Is this happening because my model doesn't take into account viscous/friction effects? The equations are:
\frac{P_1}{P_2} = e^{\beta \left[ \left( \frac{v_2}{v_1} \right)^2 -1 \right]}
\frac{A_2}{A_1} = \left( \frac{v_2}{v_1} \right)^{-1} e^{\beta \left[ \left( \frac{v_2}{v_1} \right)^2 -1 \right]}

If the gauge opening is oriented parallel to the flow, then it measures the static pressure. If it is oriented perpendicular to the flow, then it measures the total pressure (static plus dynamic).

This is so useful. I'm ashamed to admit that I had no idea we could measure dynamic pressure, not in the sense of it being impossible, I just didn't know it was common practice.

 

[Chestermiller]

Okay, here it is.
View attachment 103294
The system I described has the condition \frac{A_2}{A_1} < 1, so in order for the gas to flow from point 1 to point 2, it must operate at low \beta values. If it operated at higher \beta values the gas would flow from 2 to 1 (v_1 > v_2).

This doesn't mean that the flow is from 2 to 1. It just means that the flow is faster at point 1 than point 2.

One thing that's confusing me is that when v_1 = v_2, A_1 = A_2 and P_1 = P_2, where this last equality means there is no flow, and I'm pretty sure compressible flow of a gas in a constant area channel exists. Is this happening because my model doesn't take into account viscous/friction effects?

The last equality does not mean that there is no flow. It just means that, in inviscid flow in a pipe of constant cross section, the pressure drop is zero.

Your results are very interesting.

 

[MexChemE]

This doesn't mean that the flow is from 2 to 1. It just means that the flow is faster at point 1 than point 2.

The reason I thought the gas would flow from 2 to 1 is that due to Bernoulli's principle, if v₁ > v₂, P₂ > P₁. Can it still flow from 1 to 2 if the pressure at point 1 is lower?

The last equality does not mean that there is no flow. It just means that, in inviscid flow in a pipe of constant cross section, the pressure drop is zero.

Would this also mean that the flow becomes incompressible?

Your results are very interesting.

No doubt there's always something new to learn, that's what I love about science and engineering.

 

[Chestermiller]

The reason I thought the gas would flow from 2 to 1 is that due to Bernoulli's principle, if v₁ > v₂, P₂ > P₁. Can it still flow from 1 to 2 if the pressure at point 1 is lower?

For incompressible flow, if A1 < A2, v1 >v2, and P2 has to be greater than P1 in order to slow down the flow.

Would this also mean that the flow becomes incompressible?

No. Incompressible means that if you increase or decrease the pressure, the density won't change. This flow is just such that there is no change in pressure, even though, if the pressure changed, the density would change.

No doubt there's always something new to learn, that's what I love about science and engineering.

You're my kind of student.

 

[MexChemE]

For incompressible flow, if A1 < A2, v1 >v2, and P2 has to be greater than P1 in order to slow down the flow.

Oh, of course. Now that I remember, I've seen this happen in blood flow modeling situations.

No. Incompressible means that if you increase or decrease the pressure, the density won't change. This flow is just such that there is no change in pressure, even though, if the pressure changed, the density would change.

Alright, it's clear now.

You're my kind of student.

Thanks! And it's really nice to have a mentor around who is also a chemical engineer!