primarygun
- 233
- 0
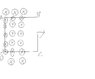
In my figure, the whole circuit is being pulled to the right.
AD experiences no change in magnetic field.
Why do we apply the Fleming's right hand rule on the loop AD instead of BC?
And, if the whole circuit is moving in the uniform magnetic field, if the shape of the circuit is like the above one, there's no induced current.
Is this also true for a circular one?
Thanks for kind attention to my thread.
I'm in urgent so I have to post here.
AD experiences no change in magnetic field.
Why do we apply the Fleming's right hand rule on the loop AD instead of BC?
And, if the whole circuit is moving in the uniform magnetic field, if the shape of the circuit is like the above one, there's no induced current.
Is this also true for a circular one?
Thanks for kind attention to my thread.
I'm in urgent so I have to post here.