Why Is My Calculated Velocity at the Swing's Apex Incorrect?

[ryho1092]

Homework Statement

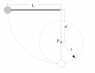
The string in the Figure is L = 113.0 cm long and the distance d to the fixed peg P is 91.5 cm. When the ball is released from rest in the position shown, it will swing along the dashed arc. How fast will it be going when it reaches the lowest point in its swing?

B-How fast will it be going when it reaches the highest point in its swing?

Homework Equations

Conservation on Energy: TE=PE+KE
KE=1/2 mv^2
PE=mgh or mg(L)---L=length of string

The Attempt at a Solution

I got 4.71 m/s for v for the first part. I got this by using conservation of energy, not moving initally and at the bottom (my reference point) no PE.

I'm stuck on the second part. I found my TE by using the starting point, mgh=PE which is 9.8 m/s^2 * 1.13m * m(mass). This should equal my PEtop + KEtop at the top, so
PEtop = mgh=mg(1.13m-.915m) and KEtop should equal 1/m2v^2. Puting it all together I have the following: TE=PE+KE 9.8m/s^2 * 1.13 m * mass = mass * 9.8 m/s^2 * (1.13-.915)m + 1/2 * mass * v^2. The masses cancle out, and I solve for v= SQRT(2*(9.8*1.13-9.8*1.13-91.5))= 4.23 m/s

But this isn't accepted by capa, what did I do wrong? Thanks in advance

Ryan

 

[SHISHKABOB]

I don't know if you meant to put up a picture, but I'm not really sure what's going on in this problem. And it looks like there's only one part?

 

[ryho1092]

My bad, thanks. I put the second part and attached a pic. Sorry

 

[ryho1092]

I see what I did wrong. I was using the PE at the top not from the pivot point. The EQ for the speed at the top of the pivot is still from TE=PE+KE TE=9.8*1.13*mass PE=9.8*.43*mass the .43 is from 1.14-.915 which gives the radius=.215 r*2=.43 This gives me 6.86 which equals KE=1/2mv^2. Then solve for v and done.