Noawun
- 1
- 0
- Homework Statement
- A glass beaker of mass 215g contains 145g of water at 18.5 degrees Celsius. If the specific heat capacity of glass is 8.4 x 10^2 J kg^-1 K^-1, how much heat energy would need to be supplied to raise the temperature of the glass and water to 98.5 degrees Celsius?
- Relevant Equations
- Q=mc\Delta T
At first, I tried to calculate the heat energy required by doing this:
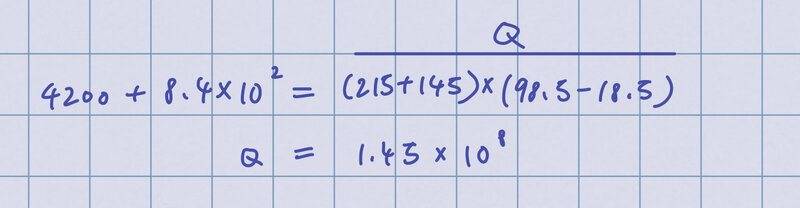
I realized I should calculate heat energy separately instead of grouping glass and water together so I did this:
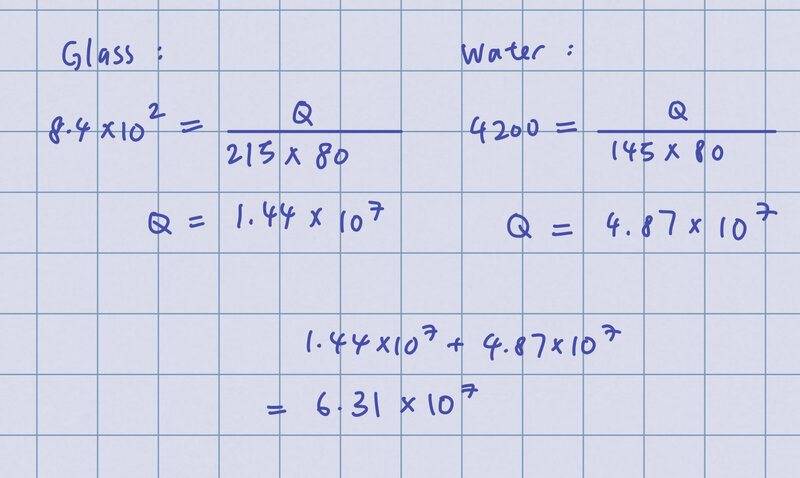
But the answer is supposed to be 6.29 x 10^4.
I don't know how to solve this. Can anyone help please? Thank you
I realized I should calculate heat energy separately instead of grouping glass and water together so I did this:
But the answer is supposed to be 6.29 x 10^4.
I don't know how to solve this. Can anyone help please? Thank you