Why is my equation of motion different from the correct one?

[TheDestroyer]

Sorry for that title, but what can I say, I'm going to be mad to get the motion equation for some systems but always failing

system 1:

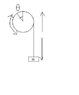
a rope rounded to a cylinder, the rope ends with a mass m and creating a pendulum with a maximum angle creating on a vibration \theta, the length of the rope while \theta = 0 is \ell, the wight of the rope is neglected

find the equation of motion using lagranges equation..

Here is the CORRET answer:

(\ell + r\theta)\ddot{\theta} + r\dot{\theta} + g sin\theta = 0

here are the steps i took, i didn't get the same result, i want some body to give me step by step,

As we know the lagrangian is:

L = T - u

and lagranges equation of motion is:

\frac{d}{dt} \frac{\partial L}{\partial \dot{q}} - \frac{\partial L}{\partial q} = 0

T is kinetic energy of the system,
u is potential energy of the system
q is a generalised coordinate

Now to find the equation of motion, we will use polar coordinates, we first find that r is constant, and the change is only in the angle so:

T = \frac{1}{2} mr^2 \dot{\theta}^2

and the potential energy is the mgh while h is the length of the rope plus the length added with the angle \theta

u = -mg(\ell + r\theta)

and now differentiating:

\frac{d}{dt} \frac{\partial L}{\partial \dot{\theta}} = \frac{d}{dt}mr^2 \dot{\theta} = mr^2 \ddot{\theta}

\frac{\partial L}{\partial \theta} = -mgr

finally, the equation of motion is:

\frac{d}{dt} \frac{\partial L}{\partial \dot{q}} - \frac{\partial L}{\partial q} = 0

mr^2 \ddot{\theta} + mgr = 0
\ddot{\theta} + \frac{g}{r} = 0

And this answer is very different to the correct one, WHY? Any one can explain? and give me the correct steps?

I'm going to give other systems later, Please anyone try GIVING ME the way to understand this mechanics .. and thanks

 

[meister]

Does the length of the rope not change as the pendulum swings? Perhaps I'm just not understanding the situation.

edit: could you maybe include a diagram?

 

[TheDestroyer]

No, the length doesn't change, but the height is changing due to the angle

 

[Dr Transport]

The cylinder is stationary, the mass swinging is the pendulum. The potential is not just mgr but mgr \cos(\theta). As the mass swings from side to side, the rope will change length giving the other term for the kinetic energy.

 

[TheDestroyer]

No man, I didn't say it's (mgr), potential energy depends on the height, I wrote the length of the rope plus the rope rounded around the cylinder because of the angle theta:

u = -mg(\ell + r\theta)

 

[TheDestroyer]

Will you exaplin more, explain everything please !

 

[Integral]

The first step is to define your coordinate system. What does \theta mean? Where is 0?

 

[TheDestroyer]

0 is in the center of the cylinder

 

[pmb_phy]

Have you tried including the rotational kinetic energy of the cylinder into T?

Pete

 

[Integral]

0 is in the center of the cylinder

I though \theta was an angle?

Your drawing seems to indicate that the cylinder is rotating? I think the problem is for a pendulum which swings off of the cylinder. Please explain your coordinate system. What is \theta ?

 

[TheDestroyer]

I've found a solution which is very near, ideas please:

if we made:

T = \frac{1}{2} mR^2 \dot{\theta}^2 = \frac{1}{2} m(\ell+r\theta)^2 \dot{\theta}^2
u = mgr(1-cos(\theta))

L = T - u = \frac{1}{2} m(\ell+r\theta)^2 \dot{\theta}^2 - mgr(1-cos(\theta))

Then substitute:

\frac{d}{dt} \frac{\partial L}{\partial \dot{\theta}} = \frac{d}{dt}m(\ell+r\theta)^2 \dot{\theta} = 2m(\ell +r\theta)r\dot{\theta}^2 + m(\ell + r\theta)^2 \ddot{\theta}

\frac{\partial L}{\partial \theta} = m(\ell + r\theta)r\dot{\theta}^2 - mgr sin(\theta)

then the equation of motion:

\frac{d}{dt} \frac{\partial L}{\partial \dot{q}} - \frac{\partial L}{\partial q} = 0

m(\ell + r\theta)^2 \ddot{\theta} + 2m(\ell + r\theta)r\dot{\theta}^2 - m(\ell + r\theta)r \dot{\theta}^2 + mgr sin(\theta) = 0

deviding by m and (\ell + r\theta)

(\ell + r\theta) \ddot{\theta} + r\dot{\theta}^2 + \frac{gr}{(\ell+r\theta)} sin(\theta)=0

WELL, the difference now is only the \frac{r}{(\ell+r\theta)}

Can anyone explain?

 

[TheDestroyer]

MY GOD, the cylinder is rotating i meant with 0 the center of the coordinates, \theta is the angle creating by the cylinder rotation in the 2 sides

 

[Integral]

This is not clear to me, where is \theta = 0 and how does it realate to the rope?

 

[Integral]

I do not think that you have a handle on the potential energy, mainly because you are misinterpreting the problem. Consider a pendulum which swings from the cylinder, \theta is the angle from the horizontal to the point of tangency of the rope. This is consistent with the initial point given in your problem definition of \theta = 0 means the length of the rope = L . To find your potential energy you need to find the distance the mass is lifted by moving the point of tangency through \theta radians. This is a geometry problem.

 

[TheDestroyer]

Well, At the height point is when \theta = 0 then potential energy is mgr, and note here, i made the beginning of the potential energy in the line containing the tangency point and the center of the cylinder, and when the pendulum moves and creates the angle \theta we will just add or subtract the length done by the angle \theta the it will be mgr\cos \theta and the difference between them is:

u = mgr - mgr\cos \theta = mgr (1-\cos \theta)

am I wrong?

 

[TheDestroyer]

This is not clear to me, where is \theta = 0 and how does it realate to the rope?

Who said \theta = 0 ?

I said the start point of the coordinates is the center of the cylinder because we are using the polar coordinates ! isn't that clear man?

 

[Integral]

Who said \theta = 0 ?

I said the start point of the coordinates is the center of the cylinder because we are using the polar coordinates ! isn't that clear man?

Clearly you do not have a grasp of the problem. The first step is to understand your coordinate system. Re read you initial post you say

a rope rounded to a cylinder, the rope ends with a mass m and creating a pendulum with a maximum angle \theta creating on a vibration , the length of the rope while \theta = 0 is L , the wight of the rope is neglected

Clearly \theta = 0 at SOME point. Remember \theta is an angle, how does it relate to the rope. Read my previous post again and think about it. If you do not understand the physical system there is no way to derive a meaningful expression for the potential and kinetic energies.

If the rope were simply moving up and down with rotations of the cylinder, then the change in potential energy would simply be r\theta since this is not the case, maybe you need to make an effort at figuring out how the system is moving.

 

[TheDestroyer]

Calm down, my english is not good, the rope length is not changing, but changing only because the theta angle,

anyone found help for me on that result? (note i didn't yet select my coordinates system, everything is going random, then i proof the correct of it)

And sorry integral if i disturbed you,

can anyone work with this problem and give me the T and U?

thanks

 

[Integral]

http://home.comcast.net/~rossgr1/Math/potential.pdf and how I see the potential energy term. I have not used it to compute the equation of motion, but perhaps this will get us on the same page as far as the coordinate system goes.

 

[TheDestroyer]

Thanks integral, i'll give a try with this height, and i'll return to tell you the result,

 

[TheDestroyer]

Thanks integral, you calculations are right, i got the answer,

 

[Integral]

EXECELLENT!

I hope that picture is of some help in undersanding where the expression for h came from. It is common in this type of problem that you must understand your coordinate system and carefully derive each expression by drawing a good diagram and aplying geometry and trigonometry.

Good luck in future problems.

BTW You may wish to contact Clausius2, he is also spanish and very knowledgeable.