Why is potential energy considered negative in an inversed pendulum system?

AI Thread Summary
In an inverted pendulum system, potential energy (PE) is defined as PE = mgz, where z is negative since the coordinate system is oriented upwards. The confusion arises from the textbook's treatment of height (h), which appears to take its absolute value, leading to questions about the reference point for zero height. The rest position of the pendulum aligns with the origin (O), which clarifies the negative work done by the pendulum due to its angle. Ultimately, the discussion highlights the importance of defining the coordinate system and reference points in understanding potential energy in this context. The thread concludes with a request to close the discussion due to the initial misunderstanding.
Andrax
Messages
117
Reaction score
0
we have an inversed pendulum(ignore the car)
cart.gif

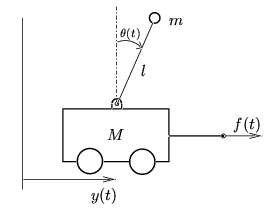
and we choose the coordinate system to be upwards
the potential energy PE=mgz (z will be hegative since( O,k) is upwards right?) z is always under O.
but in the textbook they basically take the absolute value of h i don't understand why?
 
Last edited:
Physics news on Phys.org
Where is the textbook putting the zero of h?
 
ModusPwnd said:
Where is the textbook putting the zero of h?

at the point of rest of the pendulum (same as O)
 
fixed the problem (h ad to do with angle being negatgive which means the work of p is negative)
sorry my explication of the question was off , close this thread
 

Thread '1:1 versus 2:1 Mechanical Advantage debate'

The rope is tied into the person (the load of 200 pounds) and the rope goes up from the person to a fixed pulley and back down to his hands. He hauls the rope to suspend himself in the air. What is the mechanical advantage of the system? The person will indeed only have to lift half of his body weight (roughly 100 pounds) because he now lessened the load by that same amount. This APPEARS to be a 2:1 because he can hold himself with half the force, but my question is: is that mechanical...
View full post »

Thread 'Newton's first law?'

Some physics textbook writer told me that Newton's first law applies only on bodies that feel no interactions at all. He said that if a body is on rest or moves in constant velocity, there is no external force acting on it. But I have heard another form of the law that says the net force acting on a body must be zero. This means there is interactions involved after all. So which one is correct?
View full post »
Thread 'Beam on an inclined plane'

Thread 'Beam on an inclined plane'

Hello! I have a question regarding a beam on an inclined plane. I was considering a beam resting on two supports attached to an inclined plane. I was almost sure that the lower support must be more loaded. My imagination about this problem is shown in the picture below. Here is how I wrote the condition of equilibrium forces: $$ \begin{cases} F_{g\parallel}=F_{t1}+F_{t2}, \\ F_{g\perp}=F_{r1}+F_{r2} \end{cases}. $$ On the other hand...
View full post »

Similar threads

I Change of coordinates in a potential energy field
Replies
2
Views
1K
Conservative forces, Nonconservative forces and Potential Energy
Replies
9
Views
3K
Potential Energy and Potential -- Systems versus Particles
Replies
6
Views
11K
Why is change in potential energy is always negative?
Replies
7
Views
11K
Potential Energy: Dependence on Position, Not Velocity
Replies
7
Views
2K
I Work-Energy Theorem for Moving Block and Spring System?
Replies
4
Views
2K
B Conceptually understanding change in potential energy with 0 net work
Replies
9
Views
2K
Work-KE theorem and net force....
Replies
33
Views
3K
Is Mechanical Energy Conserved for Non-Conservative Forces?
Replies
14
Views
2K
What exactly is meant by potential energy in the Lagrangian?
Replies
10
Views
2K

Hot Threads

Recent Insights

Back
Top