I Why is T+f=Ma in Cylinder Roll Without Gliding?

[Exath]

So I'm looking at a problem that involves a situation that looks like this

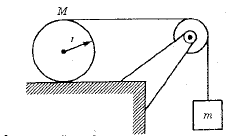
the cylinder rolls without gliding.
And there are these following equations that apply to it
(1) mg - T = ma (for the block hanging vertically)
(2) T + f = Ma (for the cylinder f = friction force, T = String force)
(3) Tr - fr = Ia (I = inertia, r = radius)

I'm only concerned about equation (2) where it's T + f = Ma, shouldn't it be T - f = Ma? Because the tension from the string and friction force are opposite to each other. It is apparently acknowledged that they are opposite in equation (3) where the torques are opposite, but why not in equation (2)?

 

[Doc Al]

I'm only concerned about equation (2) where it's T + f = Ma, shouldn't it be T - f = Ma? Because the tension from the string and friction force are opposite to each other.

Careful! The tension and friction forced are not opposite. The friction opposes slipping between surfaces, thus it acts to the right to prevent slipping of the cylinder on the table.

It is apparently acknowledged that they are opposite in equation (3) where the torques are opposite, but why not in equation (2)?

Since one force is above the axis and the other below, their torques are opposite. But the forces themselves act in the same direction.

 

[Exath]

Since one force is above the axis and the other below, their torques are opposite. But the forces themselves act in the same direction.

Ah, that's what i was looking for, i was looking at the forces the same way i was looking at torques, that's obviously wrong lol

 

[almagest]

Incidentally in (3) you need angular acceleration not linear acceleration.