Why is the number of wavelets in a slit = slit length / lambda

[DoobleD]

Hi folks,

Huygens principle is not really new to me but I just realized there is something I don't understand with it. Take a single 1D slit with a coherent incident plane wave. It seems that the number of wavelets in the slits is $n = l/\lambda$, where $l$ is the length of the slit, and $\lambda$ si the wavelength of the light. Why is it so ?

For instance, Wikipedia gives two exemples.

- a slit of length 1 wavelength has 1 wavelet :

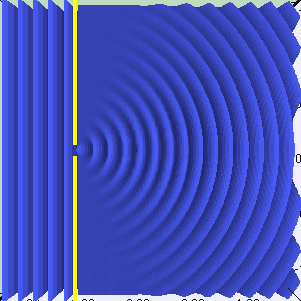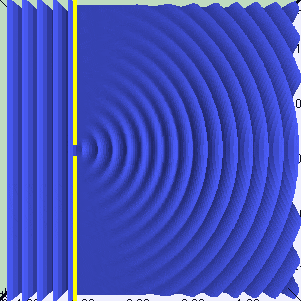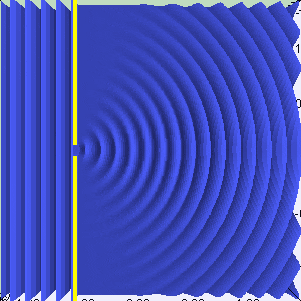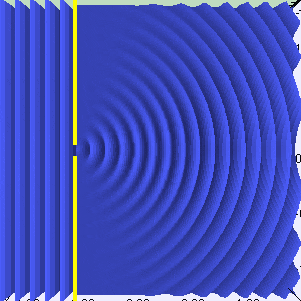
- while a slit of length 4 wavelength has 4 wavelets :

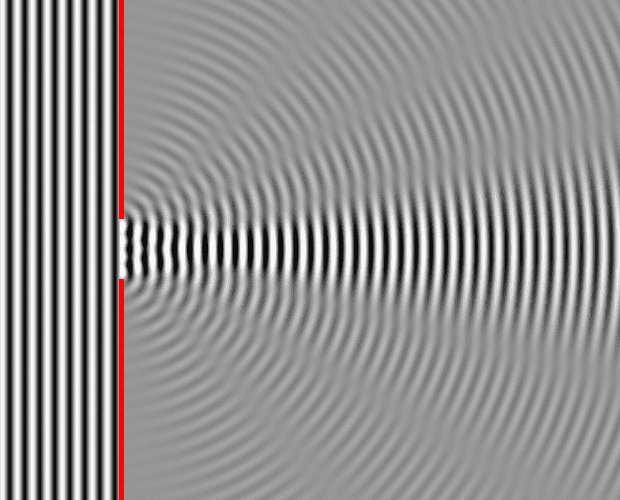
I'm looking more for some kind of intuituve explanation for the phenomenon, if there is one. I have a feeling that if we consider infinitely many wavelets in the slit, no matter it's size, they all interfere in such a way that they form a $n$ wavelets pattern. Maybe, I'm not sure.

 

[DoobleD]

Ok I' have tried some kind of simple analytical approach. Let's label the axis along the slit as $x$, and define $x = 0$ at one end of the slit. Suppose we have infinitely many wavelets in the slit. Along the slit axis, that would give an infinite sum of, say, cosines, each slightly shifted along the axis by a small amount $\delta$.

Now I try to compute that sum $s$ :

$s = \int_{0}^{l} cos(k(x - \delta))dx = \frac{1}{k}[sin(k(l - \delta)) - sin(k(0-\delta))]$

Taking $\delta \approx 0$ that would give :

$s = \frac{1}{k}sin(kl)$

So the sum would look like a sin wave of wavelength $\lambda$. Which means in a slit of size $l$, there would be indeed $l/\lambda$ pics of that sum, meaning $l/\lambda$ wavelets.

Or this might be complete gibberish, I don't know. :D What do you think ? A strange thing I did is that I used that small $\delta$ which should really be $dx$. But then I'd have a $dx$ inside the cosine, in addition to the integration one. I'm not sure what I did taking $\delta \approx 0$ like that is something legal.

 

[Ibix]

Simple answer: there are only two physically relevant length scales - the slit width and the wavelength. If there's going to be any periodic behaviour it's going to be be related to the wave character of light, so it's got to be periodic on a scale of $\lambda$.

The longer winded argument starts from Huygens' Principle that you can treat a wave as an infinite set of point sources. If you are somewhere just to the right of the slit, the electric field you see is the sum (well, integral) of the contribution of all the little sources in the slit. If you move down a little bit, all of the sources that were always above you acquire a tiny phase delay due to extra distance and a drop in brightness due to extra distance. All the sources that were always below you acquire a phase advance due to reduced distance and an increase in brightness due to reduced distance. For an incident plane wave there's no change to the contribution from the sources that were below you and are now above, by symmetry. Since the phase cycles once a wavelength, you expect some kind of periodicity at one wavelength intervals.

That's extremely hand-wavy. A better hand wave is that Huygens' Principle is $$E(x,y,z)\propto\iint E(x',y',0)\frac{e^{ikr}}r dx'dy'$$where $r$ is the distance from a point (x',y',0) in the slit to a general point (x,y,z). For a plane wave $E(x',y',0)=E_0$, and you get periodic behaviour on a length scale of $\lambda$ courtesy of the complex exponential.

 

[DoobleD]

Thank you for answering !

Simple answer: there are only two physically relevant length scales - the slit width and the wavelength. If there's going to be any periodic behaviour it's going to be be related to the wave character of light, so it's got to be periodic on a scale of λλ\lambda.

Okay the behavior is going to be related to $\lambda$, but that doesn't tell why there are specifically $l/\lambda$ wavelets in the slit. Huygens principle states that "every point on a wavefront is itself the source of spherical wavelets". So there should be infinitely many wavelets within the slit, right ? I suppose they all conspire to make $l/\lambda$ wavelets at the end. But I don't see any intuitive reason why.

A better hand wave is that Huygens' Principle is

E(x,y,z)∝∬E(x′,y′,0)eikrrdx′dy′E(x,y,z)∝∬E(x′,y′,0)eikrrdx′dy′​

E(x,y,z)\propto\iint E(x',y',0)\frac{e^{ikr}}r dx'dy'where rrr is the distance from a point (x',y',0) in the slit to a general point (x,y,z).

What I am interested in is what is the field in the slit, not really what the field looks like at a distance from a point (that point being in a slit or not). I have a feeling I could use that equation to get the field in the slit though, but can't figure out how so far.

 

[Ibix]

Okay the behavior is going to be related to $\lambda$, but that doesn't tell why there are specifically $l/\lambda$ wavelets in the slit. Huygens principle states that "every point on a wavefront is itself the source of spherical wavelets". So there should be infinitely many wavelets within the slit, right ?

What you are seeing is the places where the infinitely many point sources interfere constructively or destructively. In the plane of those sources, any periodic behaviour has to be on a scale of $\lambda$ because it's interference between waves of wavelength $\lambda$ moving in the same line (across the slit). So there are $l/\lambda$ maxima because they're $\lambda$ apart and you have distance $l$ to play with.

What I am interested in is what is the field in the slit, not really what the field looks like at a distance from a point (that point being in a slit or not). I have a feeling I could use that equation to get the field in the slit though, but can't figure out how so far.

Just set z=0. The integral over y' has to give a trivial result by symmetry, although it's not separable so it's messy.

You may wish to look up Fresnel diffraction and the Cornu spiral.

 

[DoobleD]

What you are seeing is the places where the infinitely many point sources interfere constructively or destructively. In the plane of those sources

Ok, so that's what I suspected, and it does makes sense.

any periodic behaviour has to be on a scale of λλ\lambda because it's interference between waves of wavelength λ

Oh, ok. To check that I added a few cosines of same wavelength but out of phases and graphed the sum, indeed the result also has the same wavelength ! It makes sense visually, but I never realized that.

So if I add infinitely many waves of same $\lambda$ all slightly out of phase, I should get a wave of same $\lambda$, right ? That's actually what I tried to do in my second post, but now I think the equations I wrote were non sense. I tried again :

$S(x) = \lim_{n \to \infty } \sum_{i = 0}^{n}cos(x -i\frac{L}{n}) = \int_{x'=0}^{x'=L} cos(x-x')dx'$

I tried both the sum and integral approach, and they seem to give the same result, so at least the equality between the two forms should be right. Both sum inifinitely many cosines of wavelength $2\pi$, each having an infinitesimally shifted origin with respect to the previous one, from one end of the slit ($x'=0$) to the other end ($x'=L$).

If I now solve the integral I get :

$S = sin(x) - sin(x-L)$

But if I take $L=n\lambda$, with here $\lambda = 2\pi$, then :

$S = sin(x) - sin(x-n*2\pi) = sin(x) - sin(x) = 0$ !

This can't be correct. The expected result would be a sine or cosine of wavelength $2\pi$. Any chance you see what's wrong with that simple approach ?

 

[DoobleD]

It seems I have made a mistake yesterday: the sum expression $\sum_{i=0}^n\cos\left(x-i\cdot\frac{2\pi}{n}\right)$ is apparently equal to $cos(x)$ (from Wolfram).

So the correct integral form must be different than $\int_0^L\cos\left(x-x'\right)dx'$, contrary to what I thought yesterday.

The good news is that the sum then indeed gives a cosine of wavelength $\lambda$, explaining why there are $l/\lambda$ in the slit. Now I'm trying to figure out why the integral is wrong.

 

[Charles Link]

The result of a single slit diffraction pattern is there are zeros of intensity at $m \lambda =b \sin(\theta)$ where $m$ is a non-zero integer. The maximum value of $\sin(\theta)$. A small $b$ means that $m$ is limited in size because $\sin(\theta)$ must be less than 1. $\\$ These groups of the diffraction pattern that we see that are separated by zeros of the intensity function are not Huygens wavelets. Huygens wavelets originate across the slit and are infinitesimal in their width of origin.

 

[DoobleD]

The result of a single slit diffraction pattern is there are zeros of intensity at mλ=bsin(θ)mλ=bsin⁡(θ) m \lambda =b \sin(\theta) where mm m is a non-zero integer. The maximum value of sin(θ)sin(θ) sin(\theta) . A small bb b means that mm m is limited in size because sin(θ)sin⁡(θ) \sin(\theta) must be less than 1. \\ These groups we see that are separated by zeros of the intensity function are not Huygens wavelets. Huygens wavelets are spread across the slit and are infinitesimal in their width of origin.

Yep, I know. I am not asking about the diffraction pattern, I am looking at the wavelets themselves.

 

[Charles Link]

Yep, I know. I am not asking about the diffraction pattern, I am looking at the wavelets themselves.

Again, the Huygens wavelets are infinitesimal in their geometric extent from which they originate. $n \neq \frac{l}{\lambda }$ as stated in the OP. $\\$ And again, this result is a misinterpretation that apparently was (incorrectly) concluded by looking at the nodes of the diffraction pattern.

 

[DoobleD]

Again, the Huygens wavelets are infinitesimal in their geometric extent from which they originate. n≠lλn≠lλ as stated in the OP.

Yes but they do interfere to form $n=l/\lambda$ wavelets. That's what's represented in the images of the OP. The goal of this post is precisely to understand why in fine they are $n=l/\lambda$ "wavelets-like" sources in the slit, so that we get the diffraction behavior (if we didn't have that limited number of those sources, there wouldn't be any diffraction at any scale).

 

[Ibix]

Yes but they do interfere to form $n=l/\lambda$ wavelets. That's what represented in the images of the OP. The goal of this post is precisely to understand why in fine they are $n=l/\lambda$ "wavelets-like" sources in the slit, so that we get the diffraction behavior (if we didn't have thoses limited number of those sources, there wouldn't be any diffraction at any scale).

Then you need to do the diffraction integral I quoted, or take Fresnel's approximation (I'd check if that's valid actually in the slit - I suspect not). If I understand what you are doing you are neglecting contributions from point sources with $y'\neq 0$.

 

[Charles Link]

@DoobleD Incorrect. The single slit diffraction pattern is a result of integrating $E_{total}(t)=E_o \int\limits_{0}^{b} \cos(\omega t-\frac{2 \pi \, x \, \sin{\theta}}{\lambda}) \, dx$ where $b$ is the slit width. $\\$ The intensity $I=E_{total}^2$ with the $\cos^2(\omega t)$ time dependence removed. $\\$ The $dx$ in this integral represents the width of the Huygens sources.

 

[DoobleD]

@DoobleD Incorrect. The single slit diffraction pattern is a result of integrating $E_{total}(t)=E_o \int\limits_{0}^{b} \cos(\omega t-\frac{2 \pi x \sin{\theta}}{\lambda}) \, dx$ where $b$ is the slit width. $\\$ The intensity $I=E_{total}^2$ with the $\cos^2(\omega t)$ time dependence removed.

By diffraction I meant the fact that light spreads when it goes throught the slit. If there are say 10^10000 wavelets in the slit, it does not happen, and the diffraction pattern you are referring to does not appear in that case.

EDIT : and by "wavelets" here I mean the end result that is the sum of all the infinitesimally spaced "original" wavelets which are indeed in the slit. There should be a terminology for that. Like "original wavelets" and "result wavelets" or something.

 

[Charles Link]

By diffraction I meant the fact that light spreads when it goes throught the slit. If there are say 10^10000 wavelets in the slit, it does not happen, and the diffraction pattern you are referring to does not appear in that case.

Totally incorrect. Evaluate the integral that I have given in post 13, and compute the intensity $I$ . You will find that the intensity is zero whenever $m \lambda =b \sin{\theta}$ for $m \neq 0$. $\\$ The evaluation of the integral and the computation of the intensity $I$ gives the complete diffraction pattern. It really is much simpler than it first appears.

 

[DoobleD]

Totally incorrect. Evaluate the integral that I have given in post 13, and compute the intensity II I . You will find that the intensity is zero whenever mλ=bsinθmλ=bsin⁡θ m \lambda =b \sin{\theta} for m≠0m≠0 m \neq 0 .

If $\lambda << b$ (the case where there are many "result wavelets" in the slit), what do you see on the diffraction screen ?

 

[Charles Link]

If $\lambda << b$ (the case where there are many "result wavelets" in the slit), what do you see on the diffraction screen ?

A narrow central maximum, ($\theta=0$ ), with bright regions of less intensity than the central maximum on either side of half the width of the central maximum, and then diminished intensities of successive somewhat visible spots.

 

[DoobleD]

A narrow central maximum, (θ=0θ=0 \theta=0 ), with bright regions of less intensity than the central maximum on either side of half the width of the central maximum, and then diminished intensities of successive somewhat visible spots.

You'd only see smooth light evenly spread. The interferences are there I suppose (I should have used "appear" instead of "happen"), but you don't see it. It is too small. Like when sunlight goes through a window, you can't see any diffraction pattern because the width of the window is so much bigger than the wavelength. When the wave goes through the slit, in that case, it continues as a plane wave instead of spreading, at least relatively to our scale. If we could zoom in drastically I guess we'd see the interferences though.

 

[Charles Link]

You'd only see smooth light evenly spread. The interferences are there I suppose (I should have used "appear" instead of "happen"), but you don't see it. It is too small. Like when sunlight goes through a window, you can't see any diffraction pattern because the width of the window is so much bigger than the wavelength. When the wave goes through the slit, in that case, it continues as a plane wave instead of spreading, at least relatively to our scale. If we could zoom in drastically I guess we'd see the interferences though.

You need to study and learn the mathematics behind diffraction theory, rather than to speculate what the theory is about.

 

[DoobleD]

You need to study and learn the mathematics behind diffraction theory, rather than to speculate what the theory is about.

Look, I'm not speculating anything. What you wrote on post #17 is correct, and what I wrote is correct as well: if $b >> \lambda$, the spread of the wave when it goes through the slit is too small to see, and you're eyes can't see any diffraction effect on the screen either because the fringes are too close to each other. This applies to light, water, or any wave.

As you stated, the angular positions of dark fringes are given by $m\lambda = bsin(\theta_m)$, assuming the screen is far from the slit. Let $D$ be the distance between the slit and the screen and $y$ the position of a dark fringe on the screen. Then $tan(\theta_m) = y_m/D$, so $y_m = D*tan(arcsin(m\lambda/b))$.

Let us compute the distance between 2 fringes for say $\lambda = 500 nm, b = 1 cm, D=1m$ :

$y_1 = 5*10^{-5} m, y_2 = 10^{-4} m$

If I didn't make any mistake (which I'll admit is not guaranteed), that means those dark fringes are separated by $5*10^{-5} m$. You can't see that.

Still not convinced ?

• watch Prof. Shankar explain it
• watch water waves going through a slit wider than the wavelength

Now, the initial goal of this post was for me to understand how from Huygens principle (infinitely many wavelets in the slit), we obtain $n=l/\lambda$ pics in the slit, which are also often call wavelets. Like in this simulation :

This seems to happen because all the many original wavelets add up into something that looks like only $n=l/\lambda$ wavelets in the slit.

I don't think this is new to you, I think we misunderstood each other on the term "wavelets".

 

[Charles Link]

Judging from the picture, this "wavelet" thing is a water wave phenomenon. It is not Huygens type wavelets. $\\$ And single-slit diffraction for light is not a two slit type pattern. (With a two slit pattern you can get a bunch of fringes of nearly equal intensity). In the single slit diffraction, the intensity of the first bright lobe is considerably diminished from the center bright spot, and the second lobe from center is much dimmer. $\\$ In the case of a fairly wide slit, the far field pattern will still have the central maximum, and the side lobes. With a wide slit, the far-field pattern is most readily observed by using a lens with a screen in the focal plane of the lens. If the diffraction pattern gets narrow enough, (for a wide slit), it might require a microscope or a good focal plane array of photodiodes to see all of the detail.

 

[DoobleD]

Judging from the picture, this "wavelet" thing is a water wave phenomenon. It is not Huygens type wavelets.

Right, I have used a bad terminology.

 

[Charles Link]

See also my additional comments in post 21.

 

[DoobleD]

Yes, I am aware of what single slit diffraction patterns look like and what multiple slits interference patterns look like. I did study all of that. Though I am certainly no expert of it.

 

[jbriggs444]

Judging from the picture, this "wavelet" thing is a water wave phenomenon. It is not Huygens type wavelets. \\

I may be completely out to lunch here, but it seems to me that a water wave can be treated correctly as the sum of a bunch of interfering wavelets.

 

[DoobleD]

I may be completely out to lunch here, but it seems to me that a water wave can be treated correctly as the sum of a bunch of interfering wavelets.

Yes, I see no reason why it couldn't.