- #1
Happiness
- 679
- 30
Consider a stable circular orbit (with a central force) subjected to small perturbations. The orbit equation is given by (3.45).
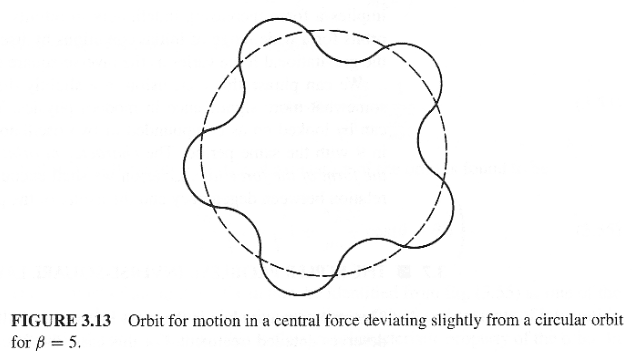
The text argues that the ##\beta## in (3.46) must be a constant over the domain of ##r_0##: "Otherwise, since ##\beta## can take on only discrete rational values (for closed orbits), the number of oscillatory periods would change discontinuously with ##r_0##, and indeed the orbits could not be closed at the discontinuity." (5th last line in the last paragraph attached below)
I don't understand this argument. I could have ##\beta=4## when ##r=r_0=1##m and ##\beta=5## when ##r=r_0'=2##m. The orbits at these values of ##r## are closed. And I can have the orbit not to be closed at other values of ##r##, which I supposed are the discontinuities referred to by the text. "Indeed the orbits could not be closed at the discontinuity." But so what? We only demand the orbit to be closed at distances ##r## where the orbit is stable and circular.
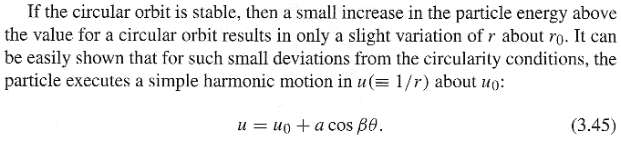
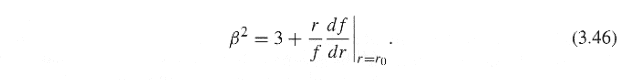

The text argues that the ##\beta## in (3.46) must be a constant over the domain of ##r_0##: "Otherwise, since ##\beta## can take on only discrete rational values (for closed orbits), the number of oscillatory periods would change discontinuously with ##r_0##, and indeed the orbits could not be closed at the discontinuity." (5th last line in the last paragraph attached below)
I don't understand this argument. I could have ##\beta=4## when ##r=r_0=1##m and ##\beta=5## when ##r=r_0'=2##m. The orbits at these values of ##r## are closed. And I can have the orbit not to be closed at other values of ##r##, which I supposed are the discontinuities referred to by the text. "Indeed the orbits could not be closed at the discontinuity." But so what? We only demand the orbit to be closed at distances ##r## where the orbit is stable and circular.
Last edited: