rjseen
- 10
- 0
Hello,
my question is, why does the decay of
K⁺ -> π⁺ ν ν-bar
require a loop to be allowed. See images below.*
-What is it that makes the decay forbidden in figure 1.4 and not forbidden in figure 1.5?
-What does being a first order weak decay and a second order weak decay mean?
-I suspect the decay is allowed in the standard model for the three modes of decay as seen in the figure 1.5. How are these modes determined?
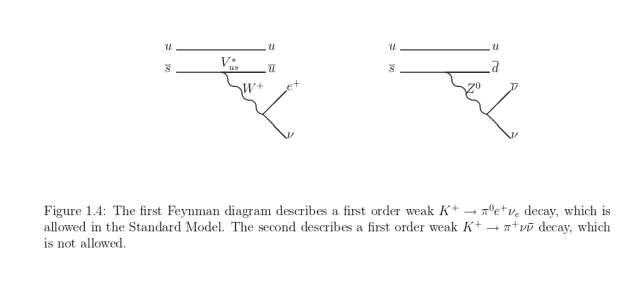
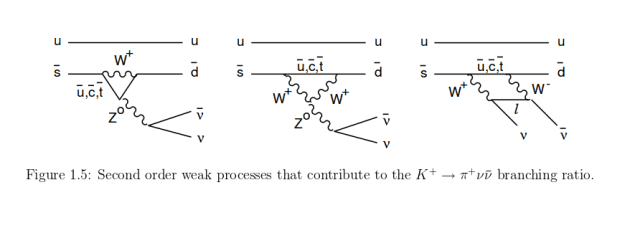
Thanks in advance,
rjseen
*With acknowledgments to Bipul Bhuyan thesis:
https://www.bnl.gov/userscenter/Thesis/2004/BB-Thesis.pdf
my question is, why does the decay of
K⁺ -> π⁺ ν ν-bar
require a loop to be allowed. See images below.*
-What is it that makes the decay forbidden in figure 1.4 and not forbidden in figure 1.5?
-What does being a first order weak decay and a second order weak decay mean?
-I suspect the decay is allowed in the standard model for the three modes of decay as seen in the figure 1.5. How are these modes determined?
Thanks in advance,
rjseen
*With acknowledgments to Bipul Bhuyan thesis:
https://www.bnl.gov/userscenter/Thesis/2004/BB-Thesis.pdf
Last edited by a moderator: