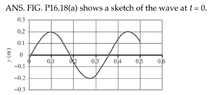
Why Wasn't (0,-3) Included in the Initial Graph of a Traveling Sinusoidal Wave?

  • Thread starter Thread starter member 731016
  • Start date Start date
  • Tags Tags
    Sinusoidal Wave
Click For Summary
SUMMARY

The discussion centers on the absence of the point (0, -3) in the initial graph of a traveling sinusoidal wave described by the equation y = Asin(kx - ωt). Participants questioned the lack of this point and the choice of graphing y against time. The conversation highlights the importance of specifying units in mathematical problems, as noted by user @BvU, and acknowledges a misunderstanding by user Callum regarding the initial conditions of the wave function.

PREREQUISITES
  • Understanding of sinusoidal wave equations, specifically y = Asin(kx - ωt)
  • Familiarity with graphing techniques for mathematical functions
  • Knowledge of wave properties such as amplitude, wavelength, and frequency
  • Basic grasp of unit measurement in physics and mathematics
NEXT STEPS
  • Research the implications of initial conditions in wave functions
  • Explore the significance of amplitude and its effect on wave graphs
  • Learn about the relationship between time and position in sinusoidal waves
  • Study the role of units in mathematical problem-solving and graphing
USEFUL FOR

Students studying physics or mathematics, educators teaching wave mechanics, and anyone interested in understanding sinusoidal functions and their graphical representations.

member 731016
Homework Statement
Please see below
Relevant Equations
y = Asin(kx - ωt)
For part(a) of this problem,
1670534765621.png

The solution is,
1670534878264.png

However, why did they not have a point at (x,y) = (0, -3) initially? Also why did they not do a y against time graph?Many thanks!
 

Attachments

  • 1670534829730.png
    1670534829730.png
    14.1 KB · Views: 137
Physics news on Phys.org
Callumnc1 said:
why did they not have a point at (x,y) = (0, -3) initially?
You sure they don't ?

1670535884436.png

##\ ##
 
Reply
  • Like
Likes   Reactions: member 731016
Callumnc1 said:
Homework Statement:: Please see below
Relevant Equations:: y = Asin(kx - ωt)

However, why did they not have a point at (x,y) = (0, -3) initially?
Your question is meaningless without units. See query by @BvU.
 
Reply
  • Like
Likes   Reactions: Scottpm and member 731016
Sorry @kuruman and @BvU, I see my mistake.

Kind regards,
Callum
 
Reply
  • Like
Likes   Reactions: BvU

Similar threads

Why does a traveling wave pulse get distorted?
  • · Replies 17 ·
Replies
17
Views
2K
Graph for sinusoidal wave travelling to the left
  • · Replies 13 ·
Replies
13
Views
2K
Sinusoidal Radiation Statements (T/F)
  • · Replies 2 ·
Replies
2
Views
1K
Voltage vs Distance graph for a given E vs D graph
  • · Replies 9 ·
Replies
9
Views
563
Location of point mass based on graphs
  • · Replies 3 ·
Replies
3
Views
1K
Finding amplitude and wave speed in a sinusoidal wave.
  • · Replies 4 ·
Replies
4
Views
2K
Graphing the Superposition of Two Standing Waves
  • · Replies 8 ·
Replies
8
Views
2K
Graphing Elastic Potential Energy
  • · Replies 10 ·
Replies
10
Views
2K
Expression y(x,t) for sinusoidal wave traveling along a rope
  • · Replies 6 ·
Replies
6
Views
4K
Phase of a wave - My interpretation
  • · Replies 4 ·
Replies
4
Views
2K