- #1
Johnls
- 11
- 0
By y I mean any perpendicular axis to the axis in which there is movement.
Thanks for the response!vanhees71 said:By definition, a boost in ##x## direction doesn't change components of four-vectors in ##y## and ##z## direction. For an introduction to special relativity, see my SRT manuscript (unfinished, but the basic concepts on Lorentz transformations are all in):
http://th.physik.uni-frankfurt.de/~hees/pf-faq/srt.pdf
Can you really? If I have a 1m rule held perpendicular to my motion and so do you, and we are on a collision course - what happens when we collide? Whose rod is shorter? Why?Johnls said:I can Imagine length contraction in the y-axis without it violating any definitions.
Johnls said:Thanks for the response!
By definition?
I can Imagine length contraction in the y-axis without it violating any definitions.
The link doesn't work for me.
Ibix said:Can you really? If I have a 1m rule held perpendicular to my motion and so do you, and we are on a collision course - what happens when we collide? Whose rod is shorter? Why?
PeroK said:Can you come up with a simple thought experiment that shows that there cannot be length contraction in the ##y## direction when the relative motion is in the ##x## direction?
Johnls said:I was about to say:
"I can imagine that in my reference frame your ruler will be shorter and in your reference frame my ruler will be shorter."
but then I realized that if I place a chalk on to top and bottom of each ruler the argument by symmetry makes perfect sense, because there should be only one result. Is this a valid thought experiment?
Here’s one example of a paradox if length contraction occurred along axes other than the direction of motion:PeroK said:Can you come up with a simple thought experiment that shows that there cannot be length contraction in the ##y## direction when the relative motion is in the ##x## direction?
y = y' follows from the Lorentz transformation for time, i.e. ##t' = \gamma (t - vx/c^2)##. An observer in the stationary frame measures a distance y in the direction perpendicular to the direction of motion (of an observer in a rocket ship) by sending a light signal from the origin (0,0) to a mirror located at position (0,y) and measuring the time, t, that it takes to return to the point (0,0). It takes t = 2y/c. But the observer in the moving rocket frame sees that same light signal travel a longer path over a time t' = 2d/c, where d is the hypotenuse of a right angle triangle whose base is v(t'/2) and whose height is y'. This is because, in the moving frame, the light is emitted at time t'=0 at a point on the x' axis (-vt'/2,0), travels to a point (0,y') and returns to a point (vt'/2,0) at a time t'.Johnls said:By y I mean any perpendicular axis to the axis in which there is movement.
Andrew Mason's example is pretty good.PeroK said:Can you come up with a simple thought experiment that shows that there cannot be length contraction in the ##y## direction when the relative motion is in the ##x## direction?
Think of the Lorentz transformation with only one dimension of space, x.Johnls said:Thanks for the response!
By definition?
I can Imagine length contraction in the y-axis without it violating any definitions.
Although, assuming the Lorentz Transformation not only jumps the gun but jumps half way to the finishing line!tade said:Most teachers jump the gun by assuming that y' = y and use it to derive time dilation, which ends up confusing students more ironically.
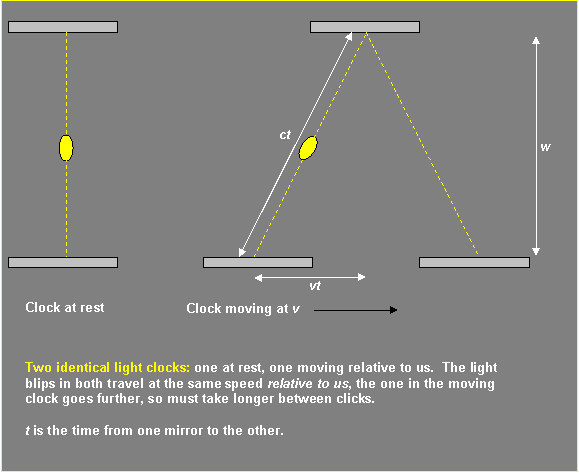
haha, but you see, teachers don't want to derive the LT the proper way, so they just skip it and use a light clock.PeroK said:Although, assuming the Lorentz Transformation not only jumps the gun but jumps half way to the finishing line!
tade said:Most teachers jump the gun by assuming that y' = y and use it to derive time dilation, working backwards, which ends up confusing students more ironically.
hmmm, I'm not so sure. there is an issue in the case of the light clock, which is time dilation being a result of the height remaining the same.robphy said:Well... it's not an unreasonable assumption since it is already there in the Galilean transformation and there has been no issues of length contraction in the Galilean case. It's only after deducing length contraction along the direction of relative motion in special relativity that one goes back and questions the assumption in the transverse direction.
tade said:hmmm, I'm not so sure. there is an issue in the case of the light clock, which is time dilation being a result of the height remaining the same.
conversely, if we assumed that there was no time dilation then there would be a height contraction of the light clock.
Although there is no height contraction in the GT, there is no length contraction either.robphy said:The issue of time-dilation arises because one is invoking the principle of relativity with the light clock...
that the round-trip of the light signal in that light clock marks one tick for that clock, as it would for a clock at rest,
but that elapsed time measured by "the clock at rest" is different than that of "the clock at rest".
While one may be so unhappy with this time-dilation result that one tries to use height-contraction to avoid it,
the arguments above show that no such height-contraction exists (as in the Galilean case, which we already presumed).
So, my point is that consideration of transverse contraction is an afterthought... since transverse-noncontraction is already practically presumed in the Galilean case.
Mmmpff! Must... resist... temptation to talk about 1-postulate derivations...tade said:The simplest assumptions would be Einstein's two postulates.


I've seen it as the "Rod and Tube Paradox". The Voigt Transforms suffer from this problem.MikeLizzi said:The sphere cannot make it through the hole. Paradox.
What does it look like when you draw a Minkowski-esque spacetime diagram and then transform it?GeorgeDishman said:I've seen it as the "Rod and Tube Paradox". The Voigt Transforms suffer from this problem.
View attachment 107973
tade said:What does it look like when you draw a Minkowski-esque spacetime diagram and then transform it?
tade said:The biggest issue with the Voigt transformations is that the primed and un-primed equations are not reciprocal.
I mean a Minkowski-esque diagram but using the Voigt transformations instead.PeterDonis said:Like there is no length contraction perpendicular to the direction of motion.
that too.PeterDonis said:The biggest issue with the Voigt transformations is that they give the wrong answers, whereas the Lorentz transformations give the right answers. Voigt didn't know that, of course; but we do.
tade said:I mean a Minkowski-esque diagram but using the Voigt transformations instead.
It would be harder to draw because you have to represent both the x and y axes as well as t so it would be a 3D image. For example I could modify this interactive diagram I did for the Twins Paradox to show a section along the axis of the rod and tube to show the wdiths 'into' the screen. As you move the slider, the widths would alter as well as the slope of the worldlines. One way, the tube gets wider and the rod narrower so all is well. Slide it the other way and the opposite happens so the rod becomes bigger than the tube and won't pass through.tade said:What does it look like when you draw a Minkowski-esque spacetime diagram and then transform it?
If y'=y/γ , then y=γy'PeterDonis said:I'm not sure you could draw one, because I don't think the Voigt transformations preserve any meaningful geometric invariants. The reason the Minkowski diagram works in SR is that the Lorentz transformations preserve the appropriate geometric invariants.
The equation y=y' in the Lorentz transformation is a result of the principle of relativity, which states that the laws of physics should be the same for all observers in uniform motion. This means that the measurements of space and time intervals should be the same for all observers, regardless of their relative velocities.
Yes, the equation y=y' is always true in the Lorentz transformation. It is a fundamental principle in the theory of special relativity and has been extensively tested and confirmed by numerous experiments.
The equation y=y' shows that space and time are relative concepts and their measurements are dependent on the observer's frame of reference. This means that what one observer perceives as a certain distance or duration may be different for another observer who is moving at a different velocity.
The derivation of y=y' in the Lorentz transformation involves the use of Lorentz equations, which describe how space and time intervals change for observers in relative motion. By using these equations, it can be shown that y=y' is a necessary result for maintaining the principle of relativity.
The equation y=y' has a significant impact on our understanding of the speed of light. It is a fundamental part of the theory of special relativity, which states that the speed of light is the same for all observers, regardless of their relative velocities. This means that the speed of light is a constant, and it is the maximum speed at which any object can travel in the universe.