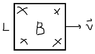
I don't know, whether I read your drawing correctly: If the entire loop moves in a homogeneous magnetic field there's indeed no work done. It just moves with constant velocity.
The usual setup is shown here in the figure with the resistor (the explanations on the webpage are not optimal, to say it friendly):
http://labman.phys.utk.edu/phys222core/modules/m5/motional_emf.html
Take the situation in this figure as the initial condition and let the wire just run without any external force. Then we can make a simple analysis to see how work is done here. We use the quasistationary approximation.
The motion of the wire induces an electromotive force according to Faraday's Law (in SI units)
$$\mathcal{E}=-\dot{\Phi}=v B d.$$
According to Ohm's law this induces a current going upwards in the wire
$$i=\mathcal{E}/R=v B d/R.$$
Now due to this current there acts a force to left on the wire, i.e.,
$$m \dot{v}=-B i d=-\frac{B^2 d^2}{R} v.$$
The power is
$$P=m \dot{v} v = -\frac{B^2 d^2}{R} v^2.$$
This is precisely the heat due to the ohmic losses in the wire,
$$P_\text{ohm}=R i^2=\frac{B^2 d^2}{R} v^2.$$
So the work done here is due to friction of the charges in the wire. It's not the magnetic field directly doing any work. It cannot do work, because the force on each charge is always perpendicular to its velocity.