zenterix
- 774
- 84
- Homework Statement
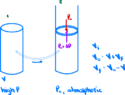
- A thin-walled metal container of volume ##V## contains a gas at high pressure. COnnected to the container is a capillary tube and stopcock. When the stopcock is opened slightly, the gas leaks slowly into a cylinder equipped with a nonleaking, frictionless piston, where the pressure remains constant at the atmospheric value ##P_0##.
(a) Show that, after as much gas as possible has leaked out, an amount of work
$$W=-P_0(V_0-V)$$
has been done, where ##V## is the volume of the gas at atmospheric pressure and temperature.
(b) How much work would be done if the gas leaked directly into the atmosphere?
- Relevant Equations
- $$W=-\int_{V_i}^{V_f} PdV$$
It seems to me that we can already answer b): if gas leaks from the high pressure container to the atmosphere, there is no expansion work. The container loses gas, which means in ##PV=nRT## we have ##n## going down and ##P## going down, and perhaps ##T## going down.
But no work.
As for a), I assume we have an approximately quasi-static process happening: the flow of gas is extremely slow such that we have approximately uniform temperature in each container individually throughout the process.
Specifically for the container with the piston, the pressure is always approximately the atmospheric pressure ##P_0##. What is really happening is that in many infinitesimally small occurrences, the pressure is ##P_0+dP##, the container expands a little bit, and the pressure goes down to ##P_0## again.
We can use equations of state for the gas in each container at every point in the process.
For the high pressure container,
$$W=-\int_V^V PdV=0$$
For the container with the piston,
$$W=-\int_{V_i}^{V_f} P_0 dV=$$
Now, ##V_0=V+V_f## then ##V_f=V_0-V##, and so if ##V_i=0##, then we get the desired result:
$$W=-P_0(V_f-V_i)=-P_0(V_0-V-0)=-P_0(V_0-V)$$
Seems to be correct, now that I wrote it all out here.
Attachments
Last edited: