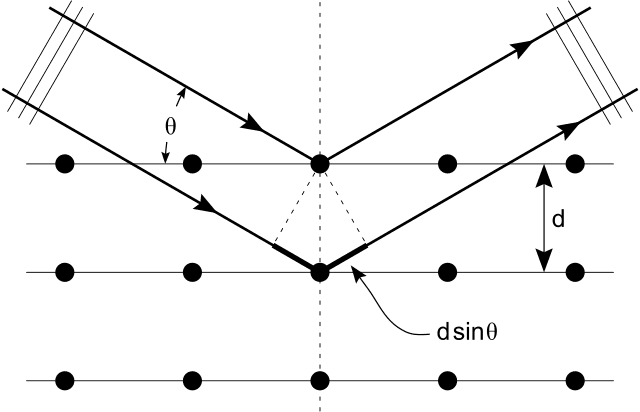
Not dumb, if you are relatively new to interference theory. Start with a large number of sources in a regular row (2 - Young's Slits - would be a way into the problem) and feed them in phase,. They will create an interference pattern with the angles of the maxima set by the wavelength and the spacing (the 2dsinθ formula). If you use an incident beam to illuminate a similarly spaced row of scattering points to try to get the same result, the only incident direction that will cause the scatterers to have a phase that's a whole number of wavelengths (equivalent to being in-phase), will be when the angle of arrival is a mirror image of the diffraction maximum. No other condition will provide the appropriate phasing of the scatterers. This is just like a mirror reflection but only for the correct angle I and R.. The deeper and wider the crystal, the sharper and better defined are the maxima. If the angle of incidence is wrong, then the scatterers do not add up coherently.
They glibly refer to the Bragg Reflection Formula but they never seemed to put it in the above way, when I learned about it. (Perhaps I just wasn't listening!)