Young's Double Slit Experiment refraction

[Prashasti]

Homework Statement

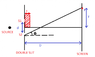
Young's double slit experiment

'd' - Separation between the two slits
'D' - Separation between the double slit and the screen
'S' - Source (Primary) (It is coherent)
S₁, S₂ - Secondary sources
Δx - Path difference between the two rays coming out from S₁ and S₂
Δx° - Path difference between the two rays coming out from S₁ and S₂ when a glass slab with refractive index μ and thickness 't' is placed in front of one of the slits.
λ - wavelength of the light waves

d<<D

2. Homework Equations

What my teacher did was,
He said that the path difference when the glass slab is kept in front of the slit would be,
Δx° = μt-t
And then he wrote,
Δx° = d sinθ - (μt-t)
And then he did the usual calculations and, finally, got
y = [nλ + (μ-1)t]D/d

I understood all the calculations he did. But I'm confused because he didn't consider the 'refraction' of light rays that pass through the slab anywhere while deriving the expression.
Won't the rays bend?
Can the lateral displacement be neglected?

 

[henxan]

Assuming D>>t it would probably be a fairly accurate description of the situation for small $\theta$. If it was me, I would place the glass on the entry-side of the slit, thus avoiding such inconsistencies.

 

[Jilang]

The light will bend towards the nornal when it enters the glass and will then bend away from the normal when it leaves the glass. The two effects will cancel and the original path will not change.

 

[Prashasti]

Assuming D>>t it would probably be a fairly accurate description of the situation for small $\theta$. If it was me, I would place the glass on the entry-side of the slit, thus avoiding such inconsistencies.

Thanks.
I got it!

 

[Prashasti]

The light will bend towards the nornal when it enters the glass and will then bend away from the normal when it leaves the glass. The two effects will cancel and the original path will not change.

No. Lateral displacement is "must", because the two media are with different refractive indices.
They won't "cancel" each other's effect...rather, the emerging ray will follow a different path. (I'm pretty sure about this)

 

[Jilang]

Yes, I absolutely see where you are coming from. The lateral displacement will tend to reduce the distance between the paths, BUT, the same angle ( the one between the normal to the glass surface and the beam) that causes the lateral displacement will also increase the time spent in the glass. Try drawing the glass surfaces at a slight angle to the beam and then rotate it a little bit. Do these effects cancel?

 

[Prashasti]

Yes, I absolutely see where you are coming from. The lateral displacement will tend to reduce the distance between the paths, BUT, the same angle ( the one between the normal to the glass surface and the beam) that causes the lateral displacement will also increase the time spent in the glass. Try drawing the glass surfaces at a slight angle to the beam and then rotate it a little bit. Do these effects cancel?

Sorry, I didn't quite understand the point. Can you explain it diagrammatically?

 

[Jilang]

If light enters the glass at 90 degrees to the planes of the glass it will go straight through with no lateral displacement. If the light goes through the glass at another angle it will have lateral displacement, but will spend longer in the glass as it has a greater distance to travel through the glass.