Young's modulus of the material

[Franco]

Hello again,
I don't understand how to derive equations.
#1
C = YI / r

Y = Young's modulus of the material
r = radius of curvature of the neutral surface
I = geometrical moment of inertia of the cross section of the beam
C = bending moment

#2
I = wt^3 / 12

I = moment of inertia
w = width of rectangular beam
t = thickness of rectangular beam

#3
Koenig's Apparatus
theta = h / 2(d+2D)

theta =angle of deflection
d = distance between mirrors on rectangular beam
D = distance between mirror(mirror which is closer to telescope) to scale
h = difference between the reading of scale


Thank you :D
i'm not good wif deriving equations :(

oh, and one more
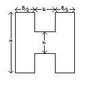
have a question asking me to arrange three beams in the order of their radius of curvature when Y, C and A are equal, the three beams are Round beam, Square beam, H-shaped beam.
i just need to find equations for moment of inertia for these shapes?

 

[Franco]

for arranging the order for three beams
for
Round beam, i have I = A^2 / 12
Square beam, i have I = A^2 / 12

with equation C = YI / r
Round beam will have r = YI / C = [Y*(A^2 / 12)] / C
Square beam will have r = YI / C = [Y*(A^2 / 12)] / C

but i don't know how to convert the H-shaped beam
i found out, for H-shaped beam
A = HB + hb
I = (BH^3 + bh^3) / 12

https://www.physicsforums.com/attachment.php?attachmentid=1682&stc=1

 

[Franco]

i've derived the other formulae
but I'm still stuck on this one, Koenig's Aparatus formula
here's a picture of it with the formula need to derive into

theta = h / [2(d+2D)]