bsodmike
- 82
- 0
First of all, is there a set means for evaluating decay energy be it an alpha, beta, or gamma decay?
Considering a means for evaluating the http://en.wikipedia.org/wiki/Decay_energy" :
Q=\left(m_0c^2\right)_{\text{after}}-\left(m_0c^2\right)_{\text{before}}
I evaluated this disintegration of Tritium into Helium-3:
^{3}_{1}T\rightarrow~^{3}_{2}He~+~e^-~+~\overline{v}_e
Considering the Tritium isotope mass is 3.0160492 u, and Helium-3 isotope mass is 3.0160293 u, \Delta m=1.99\times 10^{-5} u.
Hence, Q=(1.99\times 10^{-5}\text{u})(939.494~\text{MeV/uc\textsuperscript{2}})(\text{c\textsuperscript{2}})=18.7~\text{keV}
I have http://en.wikipedia.org/wiki/Tritium" .
However, considering the following process:
^{137}_{55}Cs\rightarrow~^{137}_{56}Ba~+~e^-~+~\overline{v}_e
This has been explained as,
and as,
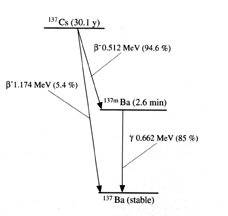
Using the earlier method I am obtaining a result of 3.9 MeV if simply considering the rest mass of both caesium-127 (136.91 u) and barium-137 (http://en.wikipedia.org/wiki/Isotopes_of_barium" ). Hence, Q=(4.188\times 10^{-3}\text{u})(939.494~\text{MeV/uc\textsuperscript{2}})(\text{c\textsuperscript{2}})=3.9~\text{MeV}
I can however see that the beta-decay to Ba-137m is simply taken from E=m_0c^2 of an electron; thus, E=(9.11\times 10^{-31}~\text{kg})(3.00\times 10^{8}~\text{ms\textsuperscript{-1}})^2=8.20\times 10^{-14}~\text{J}. Since, 1~\text{eV}=1.60\times 10^{-19}~\text{J}, this results in,
E=(8.20\times 10^{-14}~\text{J})\left(\dfrac{1~\text{eV}}{1.60\times 10^{-19}~\text{J}}\right)=0.511~\text{MeV}
I would appreciate an elucidation of the above problem; thanks in advance to contributors.
Cheers
Mike.
Considering a means for evaluating the http://en.wikipedia.org/wiki/Decay_energy" :
Q=\left(m_0c^2\right)_{\text{after}}-\left(m_0c^2\right)_{\text{before}}
I evaluated this disintegration of Tritium into Helium-3:
^{3}_{1}T\rightarrow~^{3}_{2}He~+~e^-~+~\overline{v}_e
Considering the Tritium isotope mass is 3.0160492 u, and Helium-3 isotope mass is 3.0160293 u, \Delta m=1.99\times 10^{-5} u.
Hence, Q=(1.99\times 10^{-5}\text{u})(939.494~\text{MeV/uc\textsuperscript{2}})(\text{c\textsuperscript{2}})=18.7~\text{keV}
I have http://en.wikipedia.org/wiki/Tritium" .
However, considering the following process:
^{137}_{55}Cs\rightarrow~^{137}_{56}Ba~+~e^-~+~\overline{v}_e
This has been explained as,
Cs137 decays in two ways, (1) beta-decay (maximum energy=0.518 Mev) to Ba137* followed by a gamma-transition to the ground state, and (2) beta-decay (maximum energy=1.2 Mev) directly to the ground state.
and as,
The Cs-137 parent isotope beta decays (~95%) with a 30.17y half-life to produce Ba-137m which in turn decays with a 2.55min. half-live, generating a 661.6 keV gamma ray emission.
Using the earlier method I am obtaining a result of 3.9 MeV if simply considering the rest mass of both caesium-127 (136.91 u) and barium-137 (http://en.wikipedia.org/wiki/Isotopes_of_barium" ). Hence, Q=(4.188\times 10^{-3}\text{u})(939.494~\text{MeV/uc\textsuperscript{2}})(\text{c\textsuperscript{2}})=3.9~\text{MeV}
I can however see that the beta-decay to Ba-137m is simply taken from E=m_0c^2 of an electron; thus, E=(9.11\times 10^{-31}~\text{kg})(3.00\times 10^{8}~\text{ms\textsuperscript{-1}})^2=8.20\times 10^{-14}~\text{J}. Since, 1~\text{eV}=1.60\times 10^{-19}~\text{J}, this results in,
E=(8.20\times 10^{-14}~\text{J})\left(\dfrac{1~\text{eV}}{1.60\times 10^{-19}~\text{J}}\right)=0.511~\text{MeV}
I would appreciate an elucidation of the above problem; thanks in advance to contributors.
Cheers
Mike.
Last edited by a moderator: