Zeeman effect and defining the g_F Factor

[TFM]

Homework Statement

A hydrogen atom is interacting with an external magnetic field.
1. Derive the equation for the g_F-factor of the hyperfine states.

Homework Equations

The Attempt at a Solution

Okay, so the question asks to define the gF factor, however, I am not quite sure where to start.

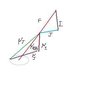
I know firstly that it is based on the diagram of the vector arrows, as (crudely drawn) attached:

I also know the answer I need to get (it is mentioned in the notes):

g_F = g_J\frac{F(F + 1) + j(j + 1) - I(I +1)}{2F(F + 1)} + \frac{\mu_N}{\mu_B}g_I \frac{F(F + 1) + I(I + 1) - j(j +1)}{2F(F + 1)}

Also, for the gJ, it starts with:

H_J = \frac{\mu_N}{\hbar}(\hat{L} + 2\vec{S})\cdot \vec{B} = \frac{\mu_N}{\hbar}(\hat{J} + \vec{S})\cdot \vec{B}

and I know for gF, we have:

H_J = \frac{\mu_B}{\hbar}(\hat{L} + 2\vec{S})\cdot \vec{B} - g_I ({\frac{\mu_N}{\hbar} \vec{I}\cdot \vec{B})

Anyone got any suggestions about what I should do first?

TFM

 

[Hao]

I suspect the approach would be to treat the external magnetic field as a perturbation to the internal magnetic field of the Hydrogen atom.

In other words, \vec{B} = \vec{B}_{Internal} + \vec{B}_{External}.

Considering \vec{B}_{Internal} first, we can find the orbital angular momentum (l), spin angular momentum (s),ml,ms (or J,m?) eigenstate of the Hamiltonian (possibly after some simplifying assumptions?).

We then apply first order perturbation theory for \vec{B}_{External}.

Since you know the energy, you should be able to get the g factor.

Hopefully, this is the way to go.