- #1
sankalpmittal
- 785
- 15
Homework Statement
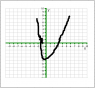
The graph of the quadratic polynomial , y=ax2+bx+c is as shown below in the figure :
http://postimage.org/image/nvkxv74yd/
Then :
(A) b2-4ac<0
(B) c<0
(C) a<0
(D) b<0
Homework Equations
y=ax2+bx+c
If y=0 , then ax2+bx+c=0
Then ,
x = {-b+-sqrt(b^2-4ac)}/2a
The Attempt at a Solution
Hmm tally image please...
When parabola is intersecting x-axis then y=0 and
Case 1 : x<0
Case 2 : x>0
if x >0 or x<0
then b2-4ac >0
So b2 > 4ac
Now what ...
Please help !
Thanks in advance.
Last edited by a moderator: