- #1
supernova1203
- 210
- 0
Net force (Diagrams incl) Please check my solutions :)
Calculate the net force acting on each object indicated in the following diagrams. Show your work.
The diagrams are in attachment, you don't have to download them to view them :)
c^2=a^2+b^2-2abCosC
c^2=√a^2+b^2
SOH CAH TOA
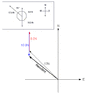
29a)
since we are given a 90 degree angle and the rest is 35 degrees, we can add
90+35
=125°
since we now have 2 sides of a triangle and the middle angle, we can use cosine to find the net force.
c^2=a^2+b^2-2abCosC
=(38)^2+(22)^2-2(38)(22)Cos125
=1444+484-1672Cos125
=1928-1672Cos125
=1928-959
c^2=√969
c=31.12 N
Fnet=31.12 N
v This 29b) is the important one, because this is where I am not sure which solution is the right one.
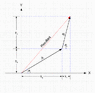
29b)
Since one side of a line has 180 degrees, and we are given 45 degrees, one can assume 180-45 degrees would give you the angle on the left side of Z.
I attempted 29b) in 2 different ways, I am not sure which one is the better way and gives the correct solution.
In method 1: i deal only with the downward vector (10 N) and the north west vector (17N)
and since 180-45=135 we have the angle in the middle, which is 135 degrees.
so using this information i use the cosine law to find the net force.
c^2=a^2+b^2-2abCosC
=(17)^2+(10)^2-2(17)(10)cos135
=289+100-340cos135
=389-240.4
=√148.6
Fnet=12.19 N
Method 2: This method, looks at the entire diagram, and assumes its one big right angle triangle.
using the smaller right triangle, we find side x.
Sin45=opposite/hypotenuse
sin45=x/75
sin45(17)=x
12.02N = x
(other side we use the given, which is 8 Newtons + 10 Newtons = 18 Newtons)
now that we have every side besides the hypotenuse we use Pythagorean to find the hypotnuse which will give us the net force.
c=√a^2+b^2
=(18)^2+(12)^2
=√324+144
=√468
c=21.63N
Fnet = 21.63 N
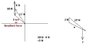
29c)
here we add the 2 given angles.
resulting in the middle angle, which is 32+24=56 °
since we have the 2 sides and the middle angle, once again we use cosine law, to find net force
c^2=a^2+b^2-2abCosC
=(15)^2 + (12)^2 -2(15)(12)Cos56
=225+144-360cos56
=√369-201.3
=√167.7
=12.94 N
Fnet= 12.94 N
Homework Statement
Calculate the net force acting on each object indicated in the following diagrams. Show your work.
The diagrams are in attachment, you don't have to download them to view them :)
Homework Equations
c^2=a^2+b^2-2abCosC
c^2=√a^2+b^2
SOH CAH TOA
The Attempt at a Solution
29a)
since we are given a 90 degree angle and the rest is 35 degrees, we can add
90+35
=125°
since we now have 2 sides of a triangle and the middle angle, we can use cosine to find the net force.
c^2=a^2+b^2-2abCosC
=(38)^2+(22)^2-2(38)(22)Cos125
=1444+484-1672Cos125
=1928-1672Cos125
=1928-959
c^2=√969
c=31.12 N
Fnet=31.12 N
v This 29b) is the important one, because this is where I am not sure which solution is the right one.
29b)
Since one side of a line has 180 degrees, and we are given 45 degrees, one can assume 180-45 degrees would give you the angle on the left side of Z.
I attempted 29b) in 2 different ways, I am not sure which one is the better way and gives the correct solution.
In method 1: i deal only with the downward vector (10 N) and the north west vector (17N)
and since 180-45=135 we have the angle in the middle, which is 135 degrees.
so using this information i use the cosine law to find the net force.
c^2=a^2+b^2-2abCosC
=(17)^2+(10)^2-2(17)(10)cos135
=289+100-340cos135
=389-240.4
=√148.6
Fnet=12.19 N
Method 2: This method, looks at the entire diagram, and assumes its one big right angle triangle.
using the smaller right triangle, we find side x.
Sin45=opposite/hypotenuse
sin45=x/75
sin45(17)=x
12.02N = x
(other side we use the given, which is 8 Newtons + 10 Newtons = 18 Newtons)
now that we have every side besides the hypotenuse we use Pythagorean to find the hypotnuse which will give us the net force.
c=√a^2+b^2
=(18)^2+(12)^2
=√324+144
=√468
c=21.63N
Fnet = 21.63 N
29c)
here we add the 2 given angles.
resulting in the middle angle, which is 32+24=56 °
since we have the 2 sides and the middle angle, once again we use cosine law, to find net force
c^2=a^2+b^2-2abCosC
=(15)^2 + (12)^2 -2(15)(12)Cos56
=225+144-360cos56
=√369-201.3
=√167.7
=12.94 N
Fnet= 12.94 N