- #1
Highway
- 349
- 1
[Dot Product] Vector Projection

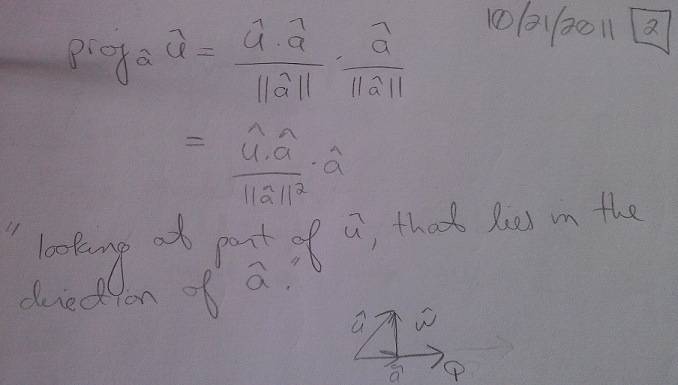
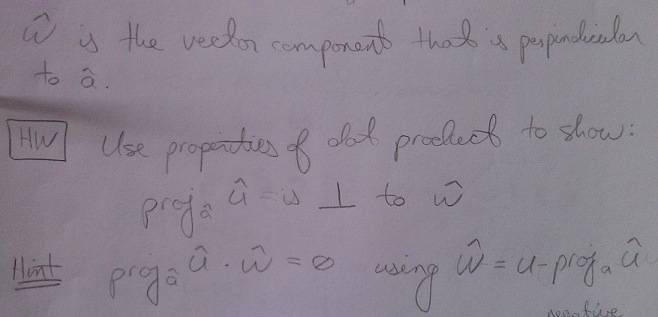
I am not sure what to do here -- I know that the projection of u onto a "dotted" with w = 0 by definition, but I don't know how to show this.
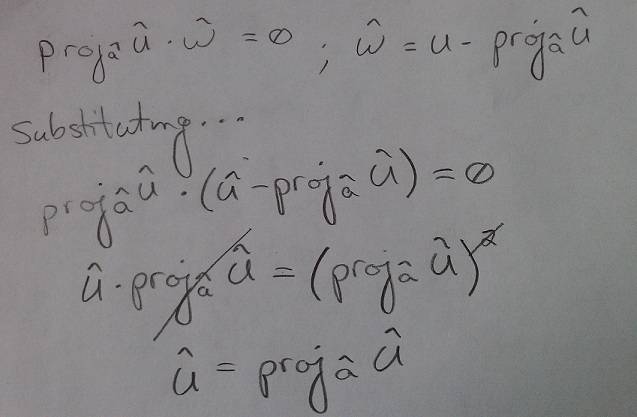
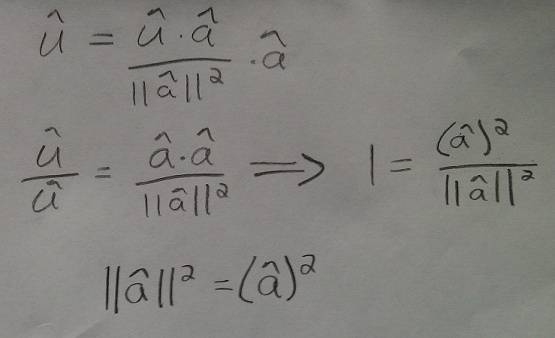
added this second part after plugging in for the definition of the projection we derived in class, then simplified. . .
Homework Statement
Homework Equations
The Attempt at a Solution
I am not sure what to do here -- I know that the projection of u onto a "dotted" with w = 0 by definition, but I don't know how to show this.
added this second part after plugging in for the definition of the projection we derived in class, then simplified. . .
Last edited: