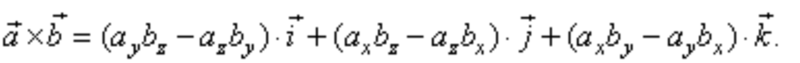- #1
greg_rack
Gold Member
- 363
- 79
- Homework Statement
- ##(\textbf{r}\times \dot{\textbf{r}})\times \textbf{r}=\dot{\textbf{r}}(\textbf{r}\cdot \textbf{r})-\textbf{r}(\textbf{r}\cdot\dot{\textbf{r}})##
Where ##\textbf{r}## is a vector
- Relevant Equations
- Vector cross and dot product
Hi guys,
I am losing my mind over this passage...
I cannot understand how to get from the first expression with the cross products to the second ##\dot{\textbf{r}}(\textbf{r}\cdot \textbf{r})-\textbf{r}(\textbf{r}\cdot\dot{\textbf{r}})##
I am losing my mind over this passage...
I cannot understand how to get from the first expression with the cross products to the second ##\dot{\textbf{r}}(\textbf{r}\cdot \textbf{r})-\textbf{r}(\textbf{r}\cdot\dot{\textbf{r}})##