- #1
nophun6
- 26
- 0
Q: The grating equation tells you at what angles different colors of light will appear: d sin θ = mλ
where d is the separation between the lines on the grating,
m is an integer (i.e., m = 0, ±1, ±2, ±3, etc.) known as the diffraction order number,
λ is the wavelength (with the same length units as d), and
θ is the angle at which light with wavelength λ is diffracted.
Make a sketch based on the figure below to show a narrow parallel beam of white light shining onto a grating with line separation d = 1150 nm. Show the angles for red and blue light for m = 0, +1, and –1 by drawing them in appropriate colors
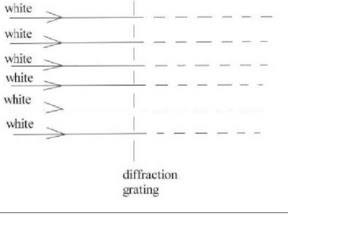
I am confused on how to start this problem. Suggestions on starting points are appreciated.
Thanks.
where d is the separation between the lines on the grating,
m is an integer (i.e., m = 0, ±1, ±2, ±3, etc.) known as the diffraction order number,
λ is the wavelength (with the same length units as d), and
θ is the angle at which light with wavelength λ is diffracted.
Make a sketch based on the figure below to show a narrow parallel beam of white light shining onto a grating with line separation d = 1150 nm. Show the angles for red and blue light for m = 0, +1, and –1 by drawing them in appropriate colors
I am confused on how to start this problem. Suggestions on starting points are appreciated.
Thanks.