Fourier Series of Even Square Wave

sandy.bridge

1. The problem statement, all variables and given/known data
[itex]-0.5\leq{t}\leq{1.5}, T=2[/itex]
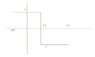
The wave is the attached picture.

I need to determine the Fourier Series of the wave in the picture.

I know that [tex]f(t)=a_0+{\sum}_{n=1}^{\infty}a_ncos(n\omega_0t)+{\sum}_{n=1}^{\infty}b _nsin(n\omega_0t)[/tex]

where [itex]a_0=\bar{f}=0[/itex] due to being an even function. Furthermore, [itex]b_n=0[/itex] due to being an even function also.

That leaves,
[tex]a_n=\int_{-0.5}^{0.5}cos(n\omega_0t)dt-\int_{0.5}^{1.5}cos(n{\omega}_0t)dt=0-\frac{1}{n\omega_0}(sin(1.5n{\omega}_0t)-sin(0.5n{\omega}_0t))=\frac{1}{n{\omega}_0}(sin(0.5n{\omega}_0t)-sin(1.5n{\omega}_0t))[/tex]

therefore,
[tex]f(t)=\frac{1}{{\omega}_0}\sum_{n=1}^{\infty}cos(n{\omega}_0t)(sin(0.5n{ \omega}_0t)-sin(1.5n{\omega}_0t))[/tex]

Is this suffice as an answer, or am I missing something? My textbook is lacking examples so I just would like to know if I am doing it right. Thanks!

Attached Thumbnails

 

sandy.bridge

I also had encountered another equation deeper in the chapter that states
[tex]f(t)=A/2+(2A/\pi)\sum_{n=1}^{\infty}\frac{sin((2n-1)\omega{_0}t)}{2n-1}[/tex]