Bernoull's Equation Derivation From Work - Energy Principle

[Dario56]

Work - Energy principle states that work of resultant force or sum of work of all forces acting on some system equals change in kinetic energy of the system.

For inviscid fluid flowing in a pipe such theorem can be used to derive Bernoulli's equation because as fluid flows it is subjected to gravity and pressure.

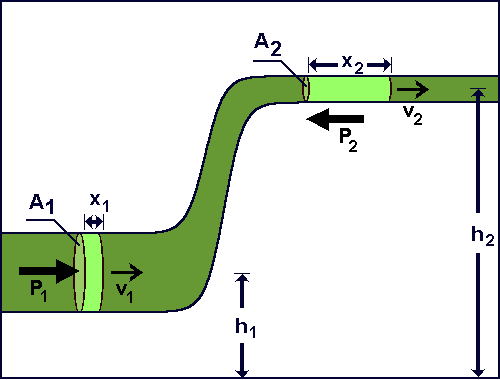
In derivation it is stated that in some time interval $\Delta t$, mass of fluid $\Delta m$ will flow through any cross section of the pipe. If we take two cross sections $A_1$ and $A_2$ which can be seen on the image, same mass flows through them in $\Delta t$ because of mass conservation. I have a problem with understanding work of pressure force. According to derivation of Bernoulli's equation, as fluid element of mass $\Delta m$ flows through cross section $A_1$, it is subjected to pressure force $F_1 = p_1A_1$ which in this cross section is in the direction of the fluid flow or displacement.

Since pressure is a scalar, it acts equally in all directions. If so, how do we know in what direction does pressure force act on the cross section? In this derivation it is stated that pressure force acts in the opposite direction on two cross - sections in the pipe scheme. Why is this so?

 

[vanhees71]

Bernoulli's equation is valid along the stream lines of the fluid elements. So you have to take the pressure force in direction of the stream lines. Since here you assume that these are perpendicular to the crossectional area of the pipes, this force is $p A$ as you write in your derivation.

 

[Lnewqban]

... Since pressure is a scalar, it acts equally in all directions. If so, how do we know in what direction does pressure force act on the cross section? In this derivation it is stated that pressure force acts in the opposite direction on two cross - sections in the pipe scheme. Why is this so?

The Pascal law still is valid for each cross section, no matter how thin we make it: pressure acts in all directions.
For a friction-less horizontal pipe of constant section, the potential and kinetic energies of the moving fluid should not change; therefore, the pressure energy should remain the same along the path, and then P1=P2.

Nevertheless, that fluid moves because some external energy or work makes it move.
That external energy is not considered by the equation that you are now studying.

Please, see:
http://hyperphysics.phy-astr.gsu.edu/hbase/pber.html

Originally, Bernoulli researched the human circulatory system.
Our vains and arteries consume internal energy of the blood due to friction, turbulences, changes of direction and velocity, obstructions, etc.
That lost energy must be constantly replenished by the mechanical work of our heart, which function is to increase the pressure energy between inlet and outlet blood.

 

[Chestermiller]

Since pressure is a scalar, it acts equally in all directions. If so, how do we know in what direction does pressure force act on the cross section? In this derivation it is stated that pressure force acts in the opposite direction on two cross - sections in the pipe scheme. Why is this so?

In freshman physics we learned that, when we do a force balance on a body or determine the work done on a body, we include only the forces exerted on it by other bodies, not the forces exerted by it on other bodies.

 

[Baluncore]

Since pressure is a scalar, it acts equally in all directions. If so, how do we know in what direction does pressure force act on the cross section?

The walls of the pipe are assumed rigid, so the complexity of the model is greatly reduced. The pressure forces applied perpendicular to the fixed pipe wall, do not move or stretch the wall, so there is no work done on the wall by the applied forces. The pipe wall pressure component is not therefore part of Bernoulli's energy accounting equation.

 

[Dario56]

In freshman physics we learned that, when we do a force balance on a body or determine the work done on a body, we include only the forces exerted on it by other bodies, not the forces exerted by it on other bodies.

Yes, that is true however since fluid flows, pressure forces on two cross sections don't act on the same mass of the fluid. Mass $\Delta m$ which goes through both cross section at time $\Delta t$ is not the same mass of the fluid and so pressure forces on two cross sections aren't applied to the same fluid element or mass. When we apply work energy principle, we want to find resultant force acting on the body and than calculate its work. But, this resultant force must act on the SAME body which isn't the case in this example as I said. This is why this derivation isn't clear to me. I like more to use Newton's 2nd law acting on fluid element to derive the equation since here force balance is written for the same fluid element as it moves along streamline.

 

[Chestermiller]

Yes, that is true however since fluid flows, pressure forces on two cross sections don't act on the same mass of the fluid. Mass $\Delta m$ which goes through both cross section at time $\Delta t$ is not the same mass of the fluid and so pressure forces on two cross sections aren't applied to the same fluid element or mass. When we apply work energy principle, we want to find resultant force acting on the body and than calculate its work. But, this resultant force must act on the SAME body which isn't the case in this example as I said. This is why this derivation isn't clear to me. I like more to use Newton's 2nd law acting on fluid element to derive the equation since here force balance is written for the same fluid element as it moves along streamline.

The system within the control volume is at steady state, so it is the same as if it is the same mass. Another way of doing all this is to do a mechanical energy balance on the material within the control volume. If the system is operating on steady state and the fluid is inviscid, the rate of change of the sum of the kinetic energy plus potential energy of the fluid within the control volume is zero. Would you like me to demonstrate how to do this energy balance?

 

[Dario56]

The system within the control volume is at steady state, so it is the same as if it is the same mass. Another way of doing all this is to do a mechanical energy balance on the material within the control volume. If the system is operating on steady state and the fluid is inviscid, the rate of change of the sum of the kinetic energy plus potential energy of the fluid within the control volume is zero. Would you like me to demonstrate how to do this energy balance?

What do you mean when you say that steady state means that we can treat both masses $\Delta m$ as being the same? I can't connect these two. While these two have the same value, pressure forces still act on different fluid elements. Also, is control volume actually volume between two cross sections? So, that we are on the same page.

Yes, I would like that if you are willling. Here is my view on energy balance which we can write for the system. Since mass in is equal to mass out (no accumulation in the control volume where control volume is a volume between two cross sections) and there is no heat and work exchanged with surroundings, energy in the system must remain constant.

However, when deriving Bernoulli's equation it is not so much about knowing that energy of fluid is constant in a control volume, but how different energy types of fluid change and turn to one another as it flows ( for example when pressure turns to kinetic energy or potential energy). In this regard, I would like to understand it more in terms of work - energy theorem than through lens of energy balance of control volume (like we often do in ChemE).

 

[Chestermiller]

I

What do you mean when you say that steady state means that we can treat both masses $\Delta m$ as being the same? I can't connect these two. While these two have the same value, pressure forces still act on different fluid elements. Also, is control volume actually volume between two cross sections? So, that we are on the same page.

Yes, I would like that if you are willling. Here is my view on energy balance which we can write for the system. Since mass in is equal to mass out (no accumulation in the control volume where control volume is a volume between two cross sections) and there is no heat and work exchanged with surroundings, energy in the system must remain constant.

However, when deriving Bernoulli's equation it is not so much about knowing that energy of fluid is constant in a control volume, but how different energy types of fluid change and turn to one another as it flows ( for example when pressure turns to kinetic energy or potential energy). In this regard, I would like to understand it more in terms of work - energy theorem than through lens of energy balance of control volume (like we often do in ChemE).

If you're a ChE, you must be familiar with Transport Phenomena by Bird, Stewart, and Lightfoot. See sections 15.2 and 15.3 on Macroscopic Mechanical Energy Balance.

I'm going to talk about the approach derived there. If the fluid is incompressible, inviscid, and the system is at steady state, then the rate of change of kinetic energy plus potential energy within the control volume is zero. The material balance tells us that $$v_1A_1=v_2A_2=\dot{V}$$where $\dot{V}$ is the volume rate of flow.

Rate of KE entering control volume $=v_1A_1\left(\rho \frac{v_1^2}{2}\right)$

Rate of KE exiting control volume $=v_2A_2\left(\rho \frac{v_2^2}{2}\right)$

Rate of PE entering control volume $=v_1A_1(\rho gz_1)$

Rate of PE exiting control volume $=v_2A_2(\rho gz_2)$

Rate of work being done by fluid upstream of control volume to force fluid into control volume $=(p_1A_1)v_1$

Rate of work being done by fluid in control volume to force fluid out of control volume $(p_2A_2)v_2$

MACROSCOPIC MECHANICAL ENERGY BALANCE:
$$\frac{d(KE+PE)}{dt}=v_1A_1\left(\rho \frac{v_1^2}{2}\right)-v_2A_2\left(\rho \frac{v_2^2}{2}\right)$$$$+v_1A_1(\rho gz_1)-v_2A_2(\rho gz_2)$$$$+(p_1A_1)v_1-(p_2A_2)v_2=0$$

 

[Dario56]

I

If you're a ChE, you must be familiar with Transport Phenomena by Bird, Stewart, and Lightfoot. See sections 15.2 and 15.3 on Macroscopic Mechanical Energy Balance.

I'm going to talk about the approach derived there. If the fluid is incompressible, inviscid, and the system is at steady state, then the rate of change of kinetic energy plus potential energy within the control volume is zero. The material balance tells us that $$v_1A_1=v_2A_2=\dot{V}$$where $\dot{V}$ is the volume rate of flow.

Rate of KE entering control volume $=v_1A_1\left(\rho \frac{v_1^2}{2}\right)$

Rate of KE exiting control volume $=v_2A_2\left(\rho \frac{v_2^2}{2}\right)$

Rate of PE entering control volume $=v_1A_1(\rho gz_1)$

Rate of PE exiting control volume $=v_2A_2(\rho gz_2)$

Rate of work being done by fluid upstream of control volume to force fluid into control volume $=(p_1A_1)v_1$

Rate of work being done by fluid in control volume to force fluid out of control volume $(p_2A_2)v_2$

MACROSCOPIC MECHANICAL ENERGY BALANCE:
$$\frac{d(KE+PE)}{dt}=v_1A_1\left(\rho \frac{v_1^2}{2}\right)-v_2A_2\left(\rho \frac{v_2^2}{2}\right)$$$$+v_1A_1(\rho gz_1)-v_2A_2(\rho gz_2)$$$$+(p_1A_1)v_1-(p_2A_2)v_2=0$$

Now, when I started a new thread related to this one, there is one thing which came to me in this derivation. To start, we used control volume approach, which is volume fixed in space and time and we watch how fluid flows in and out of it.

We started with general energy balance for the control volume. What is not clear to me is why are only kinetic and potential energy included as changing in time? What about other forms of fluid energy like pressure?

How do we define potential energy and kinetic energy in control volume since both change with position or cross section? So, if we have non - stationary flow because of which there is time change in kinetic and potential energy in control volume, in what sense do they change? Does change happen on every point or cross section or not?

 

[Chestermiller]

Now, when I started a new thread related to this one, there is one thing which came to me in this derivation. To start, we used control volume approach, which is volume fixed in space and time and we watch how fluid flows in and out of it.

We started with general energy balance for the control volume. What is not clear to me is why are only kinetic and potential energy included as changing in time? What about other forms of fluid energy like pressure?

Pressure is not a form of energy. Where did you get this crazy notion from?

How do we define potential energy and kinetic energy in control volume since both change with position or cross section? So, if we have non - stationary flow because of which there is time change in kinetic and potential energy in control volume, in what sense do they change? Does change happen on every point or cross section or not?

Before I answer this, I would like to see you take a shot at answering it. How do we define potential energy and kinetic energy within the control volume, and how do we represent the rate of change of their sum with respect to time?

 

[Dario56]

Pressure is not a form of energy. Where did you get this crazy notion from?

Before I answer this, I would like to see you take a shot at answering it. How do we define potential energy and kinetic energy within the control volume, and how do we represent the rate of change of their sum with respect to time?

Well, you know how sometimes in Bernoulli's equation, pressure is referred to as pressure energy?

My profesor did that. It has sense since pressure is included as a term along with kinetic and potential energy and Bernoulli's equation is a energy conservation statement for stationary and inviscid flow. If we define energy as ability to do work, it has sense since we saw how pressure difference can do work on fluid and cause its acceleration in very similar way how potential energy can be turned into kinetic when we for example drop some body from some height towards the ground in gravitational field of the Earth.

Well, rate of change can be said to be power. However, to define kinetic energy and potential energy in control volume can't be done unambiguously because they don't have the same value throughout the control volume.

 

[Chestermiller]

Well, you know how sometimes in Bernoulli's equation, pressure is referred to as pressure energy?

My profesor did that. It has sense since pressure is included as a term along with kinetic and potential energy and Bernoulli's equation is a energy conservation statement for stationary and inviscid flow. If we define energy as ability to do work, it has sense since we saw how pressure difference can do work on fluid and cause its acceleration in very similar way how potential energy can be turned into kinetic when we for example drop some body from some height towards the ground in gravitational field of the Earth.

I have a big problem with your professor referring to pressure as a form of energy. Shame!

Well, rate of change can be said to be power. However, to define kinetic energy and potential energy in control volume can't be done unambiguously because they don't have the same value throughout the control volume.

$$E=\int_{V_c}{\left(\rho\frac{v^2}{2}+\rho g z\right)dV}$$where v is the local magnitude of the velocity vector. $$\dot{E}=\int_{V_c}{\frac{\partial\left(\rho\frac{v^2}{2}+\rho g z\right)}{\partial t}dV}$$

 

[Dario56]

I have a big problem with your professor referring to pressure as a form of energy. Shame!

$$E=\int_{V_c}{\left(\rho\frac{v^2}{2}+\rho g z\right)dV}$$where v is the local magnitude of the velocity vector. $$\dot{E}=\int_{V_c}{\frac{\partial\left(\rho\frac{v^2}{2}+\rho g z\right)}{\partial t}dV}$$

Yes, I actually heard that it is wrong to call it that way, but it has sense and what are your thoughts on what I've written about it. Why is it wrong to consider it as an energy form of fluid? I guess answer can be found in Bird, do you know what section in the textbook discusses this question?

How you defined energy of control volume has perfect sense. Volume integral of energy sum at every point in control volume. Thank you.

 

[boneh3ad]

I have a big problem with your professor referring to pressure as a form of energy. Shame!

If done carefully, I think this is a reasonable approach, albeit one that is easily misinterpreted. Pressure is effectively a sort of potential energy stored within random molecular motions. When a fluid is accelerated, some of this is converted into organized motion.

 

[Chestermiller]

If done carefully, I think this is a reasonable approach, albeit one that is easily misinterpreted. Pressure is effectively a sort of potential energy stored within random molecular motions. When a fluid is accelerated, some of this is converted into organized motion.

Sorry. It doesn't resonate with me.

 

[Dario56]

If done carefully, I think this is a reasonable approach, albeit one that is easily misinterpreted. Pressure is effectively a sort of potential energy stored within random molecular motions. When a fluid is accelerated, some of this is converted into organized motion.

Yes, this is how I view it. In this regard, it is similar to any potential energy type.

 

[russ_watters]

"Pressure energy" is a term used pretty frequently in the context of Bernoulli's principle/equation. To be precise, pressure is not a form of energy and the terms in Bernoulli's equation are not types of energy -- they are energy per unit volume. I guess it's a shorthand vs calling it "pressure energy per unit volume".

See also, a prior thread on the subject you guys participated in:
https://www.physicsforums.com/threads/in-fluid-mechanics-what-does-pressure-energy-mean.866534/

 

[boneh3ad]

Sorry. It doesn't resonate with me.

For adiabatic, quasi-1D flow through a streamtube with no viscous or shaft work, you can reduce the energy equation to the two equivalent forms:
$$d\left[ \frac{p}{\rho} + u + \frac{|v|^2}{2} \right] = 0$$
or
$$d\left[ h + \frac{|v|^2}{2} \right] = 0$$
where $\vec{v}$ is velocity, $p$ is the thermodynamic (static) pressure, $\rho$ is density, $u$ is specific internal energy, and $h$ is specific enthalpy. If you assume the flow is incompressible and adiabatic, $u=c_p T$ is going to be constant and therefore $p/\rho$ is the only quantity within $h$ varying in the flow. In essence, $\Delta p \propto \Delta h$ under these conditions. So in that sense, the idea of pressure energy is useful, if inexact, and specifically applies under the conditions required to derive Bernoulli's equation.

That $p/\rho$ term also has units of specific energy and is a primary component of specific enthalpy, which is used as a type of energy. I'd at least describe it as "energy-like."

 

[Dario56]

Sorry. It doesn't resonate with me.

Here is how I see it. Pressure can be defined as system's ability to do work via volume change. Since energy is defined as ability to do work, pressure is a form energy.

However, what isn't clear is that, in the derivation of Bernoulli's equation by control volume approach, pressure didn't enter the definition of fluid energy within control volume and in that regard can't be considered a form of energy.

What are your thoughts about this question?

 

[vanhees71]

If done carefully, I think this is a reasonable approach, albeit one that is easily misinterpreted. Pressure is effectively a sort of potential energy stored within random molecular motions. When a fluid is accelerated, some of this is converted into organized motion.

Conceptually pressure is part of the stress tensor of the fluid. From the relativistic point of view it's related to energy and momentum, because it's, given a reference frame, the space-space components of the energy-momentum-stress tensor and thus naturally occurs in the momentum balance, which is identical with the equation of motion e.g., the Euler equation for the ideal fluid. In the latter pressure thus occurs in some sense as a potential of a force density.