Bessel Function Boundary Condition on the top of a Cylinder

[Othman0111]

Hi everyone,

I'm working through the boundary conditions and I could not figure out what to do with the last boundary condition (when z=L)

I know that the values for K are:

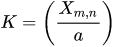
How so?

1. Homework Statement

A hollow right angle cylinder of radius a and length l. The sides and bottom are grounded. The potential at the top of the cylinder
is

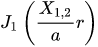where X_1,2 is the second zero of the first Bessel function. (Note:
the potential on the top of the cylinder is cylindrically symmetric)
a) Find the potential everywhere inside the cylinder. Find the charge
density on the surface of the cylinder.

Homework Equations

Bessel function relations, probably something have to do with the orthogonality.

The Attempt at a Solution

 

[Dr Transport]

what is $r$?

 

[Othman0111]

what is $r$?

It supposed to be a ρ

 

[Dr Transport]

Where did you get the original expression for the potential? My expression for the potential in Jackson is a little different.

 

[Othman0111]

Where did you get the original expression for the potential? My expression for the potential in Jackson is a little different.

The general expression of Φ shown here on this similar problem.

 

[Dr Transport]

that doesn't look right, the last two summations are usually combined and what text quoted that expression? You cannot get a $J_1(\kappa\rho)$ from a sum over $J_0(\kappa\rho)$'s. The entire problem should be shown, something looks fishy.

 

[Othman0111]

that doesn't look right, the last two summations are usually combined and what text quoted that expression? You cannot get a $J_1(\kappa\rho)$ from a sum over $J_0(\kappa\rho)$'s. The entire problem should be shown, something looks fishy.

There is no Φ dependence → 2nd and 4th summation goes to zero.
The remaining term is after applying boundary conditions and absorbing the constants into one constant is : Φ(ρ,z) = ΣAok J0(Kρ) sinh(Kz)
After applying the last boundary condition " Φ(ρ,z=L) " is:

>
The solution that I uploaded in the last comment was not for this problem, it was for a similar problem that state:

Problem 1: A hollow right angle cylinder of radius a and length l has both
ends and the sides grounded except for a band in the middle of the side of the
cylinder. The band in the middle is held at a potential of V0 and extends from
the center of the side of the cylinder for a distance of l=4 in both directions.
a) Find the potential everywhere inside the cylinder.

 

[Dr Transport]

A problem very similar to this I have seen online and your expression for the potential is not correct to do the problem as stated in my opinion.

 

[Othman0111]

A problem very similar to this I have seen online and your expression for the potential is not correct to do the problem as stated in my opinion.

Could you please give me the like to that problem. Or give me more guidance.

 

[Dr Transport]

if you do a search for potential cylindrical coordinates, you should find something, we are not supposed to give out solutions carte blanche. I'll say that your expression for the potential is not correct as written.

 

[Othman0111]

if you do a search for potential cylindrical coordinates, you should find something, we are not supposed to give out solutions carte blanche. I'll say that your expression for the potential is not correct as written.

I didn't find it in Jackson either. But it was what professors taght us to do. The homework is due but I just were curious. Thank you, sir.
Attached a PDF version of his notes, the equation is on page 21.

Regards

 

[TSny]

I'm not sure which edition of Jackson you have. For the 3rd edition see section 3.8, pages 117 and 118. You should be able to use equations (3.105a) and (3.105b) to determine the potential inside the cylinder. In your problem, the potential does not depend on $\phi$. So, only one value of the index $m$ in (3.105a) contributes.

 

[TSny]

You cannot get a $J_1(\kappa\rho)$ from a sum over $J_0(\kappa\rho)$'s.

It turns out you can. I wasn't sure and I had to take some time to review this. But you can essentially expand an "arbitrary" function $f(x)$ over the interval $0<x<a$ in terms of Bessel functions of a single order, say Bessel functions of zeroth order. So, you can expand $J_1(x)$ on $0<x<a$ in terms of the infinite set of functions $\left \{ J_0(\frac{X_{0,k}}{a}x), k = 1, 2, 3, .. \right \}$, where $X_{0, k}$ is the $k$^th zero of $J_0(x)$.

See
https://www.math.upenn.edu/~rimmer/math241/ch12sc6frbess.pdf

 

[Othman0111]

I'm not sure which edition of Jackson you have. For the 3rd edition see section 3.8, pages 117 and 118. You should be able to use equations (3.105a) and (3.105b) to determine the potential inside the cylinder. In your problem, the potential does not depend on $\phi$. So, only one value of the index $m$ in (3.105a) contributes.

View attachment 239655

View attachment 239656

It turns out that I don't know much about Bessel function. Thank you, sir.