- #1
Abhishek11235
- 175
- 39
Homework Statement
The problem is taken from Morin's book on classical mechanics. I found out Lagrangian of motion. Now to solve, we need small angle and small x approximation. The small angle approximation is easy to treat. But how to solve small x approximation i.e how do I apply it?
Homework Equations
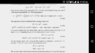
Given ##x/l \lt\lt 1## we need to solve:
$$Ml^2\ddot\theta +ml(l\ddot\theta + \ddot x)+mx^2\ddot\theta+2mx\dot\theta\dot x=-(M+m)glsin\theta - mgxcos\theta$$
The Attempt at a Solution
[/B]
I tried to divide whole expression and since ##x\lt\lt
Attachments
Last edited by a moderator: