Find the modulus and argument of ##\dfrac{z_1}{z_2}##

[chwala]

Homework Statement

See attached

Relevant Equations

Complex numbers

π

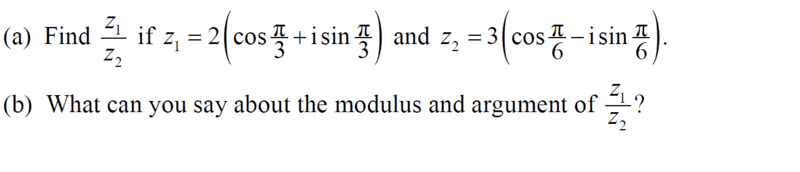
My take; i multiplied by the conjugate of the denominator...

$$\dfrac{z_1}{z_2}=\dfrac{2(\cos\dfrac{π}{3}+i \sin \dfrac{π}{3})}{3(\cos\dfrac{π}{6}+i \sin \dfrac{π}{6})}⋅\dfrac{3(\cos\dfrac{π}{6}-i \sin \dfrac{π}{6})}{3(\cos\dfrac{π}{6}-i \sin \dfrac{π}{6})}=\dfrac{2(\cos\dfrac{π}{3}+i \sin \dfrac{π}{3})}{3}⋅\dfrac{3(\cos\dfrac{π}{6}-i \sin \dfrac{π}{6})}{3}$$

...This will also realise the required result;though with some work by making use of,

$\cos a⋅\cos b-i\cos a⋅\sin b + i\sin a⋅cos b + \sin a⋅\sin b$

$=\cos a⋅\cos b+\sin a⋅\sin b-i\cos a⋅\sin b+i\sin a⋅\cos b$

$=\cos(a-b)-i\sin (a-b)$

for our case, and considering the argument part of the working we shall have,

$=\cos\left[\dfrac{π}{3}- - \dfrac{π}{6}\right]-i(\sin \left[\dfrac{π}{3}- - \dfrac{π}{6}\right]= \cos\left[\dfrac{π}{3}+\dfrac{π}{6}\right]-i(\sin \left[\dfrac{π}{3}+\dfrac{π}{6}\right]$

$=\cos\left[\dfrac{π}{2}\right]-i\sin \left[\dfrac{π}{2}\right]$

 

[pasmith]

Use $$\cos \theta + i\sin \theta = e^{i\theta}.$$

 

[chwala]

Use $$\cos \theta + i\sin \theta = e^{i\theta}.$$

Fine, let me check on this again...

 

[chwala]

$\dfrac{z_1}{z_2}=\dfrac{2}{3}e^{i\left[\dfrac{π}{3}+\dfrac{π}{6}\right]}=\dfrac{2}{3}e^{i\left[\dfrac{π}{2}\right]}$

Therefore

Modulus =$\dfrac{2}{3}$

and

Argument= $\dfrac{π}{2}$