- #1
Francisco Alegria
- 2
- 0
- TL;DR Summary
- I want to determine a specific identity involving gamma matrix and four vectors
Is the fowwowin identity correct for a generic four-vector"q"? What is the proof? Thank you.
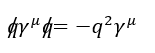
##\not{\!p}## is produced by typing "\not{\!p}".vanhees71 said:[Note: Is there some equivalent of "slashed" from the LaTeX package slashed.sty to type "Feynman slashes"?]
Gamma matrices are mathematical objects used in the study of quantum mechanics and special relativity. They are a set of 4x4 matrices that represent the four-dimensional space-time coordinates of a particle. In identity with four-vector contractions, they are used to simplify and manipulate equations involving four-vectors.
Gamma matrices are important in physics because they allow us to describe and understand the behavior of particles in the context of special relativity. They are used in a variety of calculations and equations, including those involving spin, angular momentum, and energy. Without them, many important concepts in modern physics would be much more difficult to understand and explain.
Four-vector contractions are mathematical operations that involve multiplying and summing over the components of four-vectors. In the context of identity with Gamma matrices, they are used to simplify and manipulate equations involving four-vectors and Gamma matrices. This allows us to solve problems and make predictions about the behavior of particles in special relativity.
The Lorentz transformation is a mathematical formula that describes how the coordinates of an event in space-time change when viewed from different inertial reference frames. Gamma matrices and four-vector contractions are used in the derivation and application of the Lorentz transformation, as they are essential tools for understanding the effects of special relativity on particles and their coordinates.
One practical application of Gamma matrices and four-vector contractions is in the calculation of the magnetic moment of a particle. The magnetic moment is a measure of the strength and orientation of a particle's magnetic field, and it can be determined using equations that involve Gamma matrices and four-vector contractions. This allows us to make predictions about how particles will behave in magnetic fields, which has important applications in fields such as particle accelerators and magnetic resonance imaging (MRI) technology.