Lagrangian with angular velocity not constant

[pepediaz]

Summary:: not constant spin

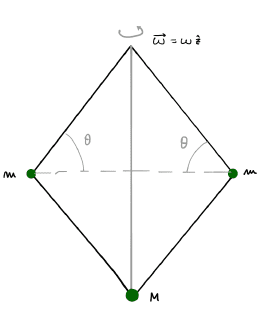
How could I calculate the system lagrangian in function of the generalised coordinates and the conserved quantities associated to the system symmetries?

I've been struggling for the case with not constant angular velocity, but I don't realize what I have to do.

Thanks in advance

 

[vanhees71]

It's not so clear to me, what exactly you want to describe. Are the three masses connected with four (massless?) rigid rods and fixed to rotate around the drawn vertical line? If so, you only need to describe the motion of the two masses $m$ parametrizing their location with the rotation angle $\phi$ around the vertical axis. In this case the EoM will of course tell you that $\omega=\text{const}$ due to the conservation of the angular momentum component in direction of the vertical axis.

 

[pepediaz]

Yes, as you describe, the masses are connected with four massless rods and the system rotates around the z axis. I've already solved it supposing ω=const, but now I have to take out the constraint that implies ω=const. So, the rotational motion this way results not constant?

 

[vanhees71]

Which constraint? You should show your work, so that I can see where the problem is.

 

[pepediaz]

I solved it as shown supposing ω=const as a holonomic constraint, or restriction. Now I have to take out this constraint, so, the rotational motion will become not constant and the lagrangian changes, isn't it?

 

[vanhees71]

Now I understand (the formula density is high enough ;-)). The mass, $m_2$, is additionally free to glide along the $y$ axis, and you enforce the entire construction to spin with constant angular velocity around the $y$ axis.

If you want to have a non-constant $\omega$ then you can just write $\phi(t)$ instead of $\omega t$ in (3.106), with a given function $\phi(t)$. That'll be not so easy to solve though (depending on the function you have).

 

[pepediaz]

I see, but that function ϕ(t), it has to be defined previously as a certain function, or i can use it as a generalised coordinate?

 

[vanhees71]

These are two different questions: If you put a predefined function you describe the situation where from the outside you force the construction to rotate according to this given function of time.

If you leave $\phi$ as a generalized coordinate, you just look at the motion of the entire system given an initial condition without any external enforcement of this degree of freedom. That's also a very nice exercise, I guess. You can study the conservation laws and Noether's theorem with it (looking at the symmetries the system has of course).

 

[pepediaz]

I understand. For looking at the symmetries, could you give an example of the use of Noether's theorem for a certain current? I am trying to obtain the symmetries of the lagrangian shown in the pictures, and I can't clear up its working.

 

[vanhees71]

Well, there's the obvious symmetry under rotations around the $y$-axis (which are parametrized with your angle $\phi$). Just write down the Lagrangian and check what this implies!

 

[pepediaz]

We notice ϕ is a cyclic coordinate and thus we note that the constant term we get is the y-component of the angular momentum. Nevertheless, for the case with ω=const shown in pictures, as i have used θ as a generalised coordinate, I don't have terms with x in the lagrangian, so when I have to show if there is translational symmetry or not, I don't know if I have to redo the lagrangian using x as a generalised coordinate and see if it is cyclic, or if Noether theorem (or Poisson brackets, though I think it would be similar) can give me the symmetry from the lagrangrian I already have.

 

[vanhees71]

The system obviously has two independent degrees of freedom. I'd use $\theta$ and $\phi$ for the case without external rotation around the $y$ axis. It's of course clear that $\phi$ is cyclic due to the rotation symmetry around the $y$ axis, and that's a special case of Noether's theorem, where the symmetry transformation is simply given by "translation" in the generalized coordinate, i.e., the symmetry transformation is simply given by $\phi \rightarrow \phi + \alpha$.

The 2nd symmetry is time-translation invariance leading to energy conservation.

 

[pepediaz]

I see, and how can I proof those two invariances by application of Noether's theorem?

 

[vanhees71]

Just do the "infinitesimal" time or $\phi$ translations of the action.

 

[pepediaz]

You mean substituting ϕ with ϕ+α in the lagrangian, in this case?
Supposing α = const, the lagrangian remains the same, so, the problem comes when verifying the symmetry for translations of coordinate x, I mean, for proving if linear momentum is conserved or not.
For the particular case of time invariance, I had thought calculating energy function h = pq - L and comparing if it is the same than hamiltonian H = T + U.

 

[wrobel]

Deriving the energy integral from Noether's theorem needs some effort. Let a Lagrangian $L=L(x,\dot x),\quad x=(x^1,\ldots,x^m)$ be independent on $t$. We also have the Action functional $x(\cdot)\mapsto\int_{t_1}^{t_2}Ldt$. Let's change the time here
$$t=t(\tau),\quad \int_{t_1}^{t_2}Ldt=\int_{\tau_1}^{\tau_2}L\Big(x,\frac{x'}{t'}\Big)t' d\tau,\quad x':=\frac{dx}{d\tau},\quad t':=\frac{dt}{d\tau}.$$
This provides us with a new Lagrangian system with generalized coordinates $y=(x^1,\ldots,x^m,t)$ and with the Lagrangian
$$\mathcal L(y,y')=L\Big(x,\frac{x'}{t'}\Big)t'.$$
This Lagrangian does not depend on the coordinate $t$, so that there is the first integral

$$\frac{\partial\mathcal L}{\partial t'}=L-\Big(\frac{\partial L}{\partial \dot x},x'\Big)\frac{1}{t'}=L-\Big(\frac{\partial L}{\partial \dot x},\dot x\Big)=-H$$

 

[pepediaz]

So, this way is how we prove the invariance on time of the system, be ω=const or not, isn't it?

 

[pepediaz]

I can't realize how I can extrapolate your development to prove the invariance (or not invariance) on galilean boosts or translations of the system.

 

[JD_PM]

the problem comes when verifying the symmetry for translations of coordinate x, I mean, for proving if linear momentum is conserved or not.

I'd recommend trying to do so explicitly.

You'll need to pick $b$ as your generalized coordinate (see image below) and get your Lagrangian.

You should get kinetic energy terms like $m_1 \dot b^2$ and $m_1 b^2 \omega^2$...

Once you get the Lagrangian you'll see at first glance whether momentum is conserved in the x-direction or not.