- #1
HansBu
- 24
- 5
- Homework Statement
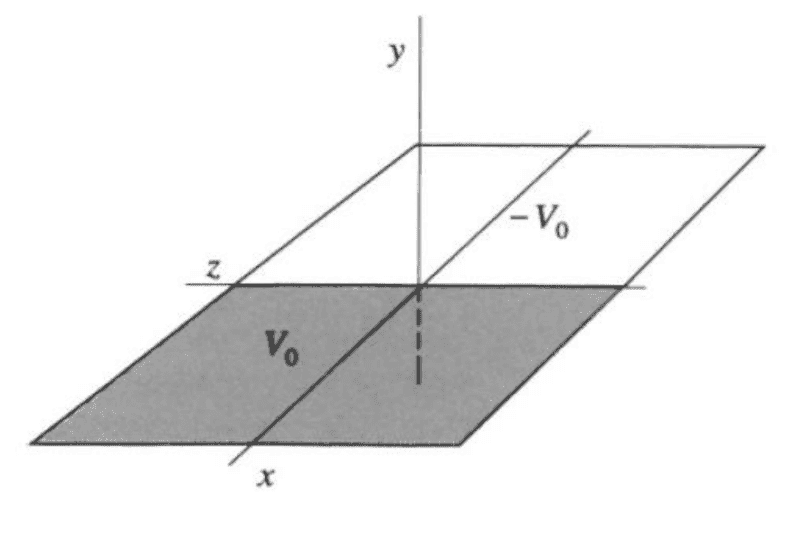
- Determine the potential and electric field at any point due to an infinite conducting plane lying in x-z plane. Half of the plane (x > 0) is maintained at +Vo while the other half (x < 0) is maintained at -Vo.
- Relevant Equations
- A relevant equation would include Laplace's Equation for Electrostatic Problems.
I really have no idea as to how to attack the problem in the first place. I am here to ask for some generous help on how to start. The figure is shown below for reference.