- #1
Saladsamurai
- 3,020
- 7
Hello!  I am going over an example in my fluid mechanics text and I am confused about a few lines. My question is more about the math then the fluid mechanics. In fact, I doubt you need to understand the FM at all; if you understand Diff eqs, you can probably answer my question.
I am going over an example in my fluid mechanics text and I am confused about a few lines. My question is more about the math then the fluid mechanics. In fact, I doubt you need to understand the FM at all; if you understand Diff eqs, you can probably answer my question.
I am given the components of the velocity field:
[tex]u = a(x^2-y^2)\,\,\,\,\,\,\,\,\,\,\,v = -2axy\,\,\,\,\,\,\,\,\,\,w=0[/tex]
and I am also given that gravity only acts in the downward z direction [itex]g_z = -g[/itex].
The example question asks to first determine under what conditions the given velocity field is a solution to the Navier-Stokes equation. Then, assuming that these conditions are met, determine the resulting pressure distribution p(x,y,z).
The Navier-Stokes EQs are given by:
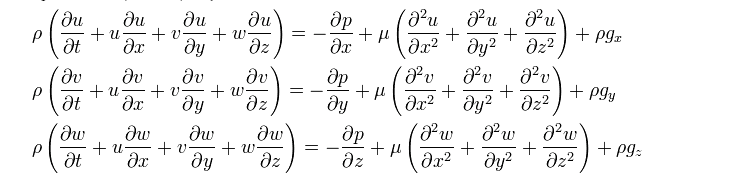
Their approach is as follows. They say
1st question: what do they mean by exact? What would it mean to not be exact?Alright, now after a whole bunch a solving that you don't need to see, we end up with the following pressure gradients:
[tex]\frac{\partial{p}}{\partial{x}}=-2a^2\rho(x^3+xy^2)[/tex]
[tex]\frac{\partial{p}}{\partial{y}}=-2a^2\rho(x^2y+y^3)[/tex]
[tex]\frac{\partial{p}}{\partial{z}}=\rho g[/tex]
The book then says:
2nd question Why do I need to do this? What do they mean compatible? I know that this is reminisce of an 'exact diff EQ,' but I don't really know what that means ... I just know how to solve one by going through the motions.
So we then go ahead and cross-differentiate and find that
[tex]\frac{\partial{}}{\partial{y}}(\frac{\partial{p}}{\partial{x}}) = \frac{\partial{}}{\partial{x}}(\frac{\partial{p}}{\partial{y}})[/tex]
But I still do not know why we care. And secondly, why don't we cross-differentiate
[tex]\frac{\partial{p}}{\partial{z}}=\rho g[/tex]
with anything?
Any insight would be greatly appreciated.
~Casey
I am given the components of the velocity field:
[tex]u = a(x^2-y^2)\,\,\,\,\,\,\,\,\,\,\,v = -2axy\,\,\,\,\,\,\,\,\,\,w=0[/tex]
and I am also given that gravity only acts in the downward z direction [itex]g_z = -g[/itex].
The example question asks to first determine under what conditions the given velocity field is a solution to the Navier-Stokes equation. Then, assuming that these conditions are met, determine the resulting pressure distribution p(x,y,z).
The Navier-Stokes EQs are given by:
Their approach is as follows. They say
Assume steady state flow and let viscosity [itex]\mu[/itex] and density [itex]\rho[/itex] be constant. Substitute the known (u, v, w) into the N-S equations and solve for the pressure gradients. If a unique pressure function p(x,y,z) can be found, the given solution is exact.
1st question: what do they mean by exact? What would it mean to not be exact?Alright, now after a whole bunch a solving that you don't need to see, we end up with the following pressure gradients:
[tex]\frac{\partial{p}}{\partial{x}}=-2a^2\rho(x^3+xy^2)[/tex]
[tex]\frac{\partial{p}}{\partial{y}}=-2a^2\rho(x^2y+y^3)[/tex]
[tex]\frac{\partial{p}}{\partial{z}}=\rho g[/tex]
The book then says:
The vertical pressure is hydrostatic since w=0. To determine if the x and y gradients of pressure are compatible, evaluate the mixed derivative; that is cross-differentiate the two EQs.
2nd question Why do I need to do this? What do they mean compatible? I know that this is reminisce of an 'exact diff EQ,' but I don't really know what that means ... I just know how to solve one by going through the motions.
So we then go ahead and cross-differentiate and find that
[tex]\frac{\partial{}}{\partial{y}}(\frac{\partial{p}}{\partial{x}}) = \frac{\partial{}}{\partial{x}}(\frac{\partial{p}}{\partial{y}})[/tex]
But I still do not know why we care. And secondly, why don't we cross-differentiate
[tex]\frac{\partial{p}}{\partial{z}}=\rho g[/tex]
with anything?
Any insight would be greatly appreciated.
~Casey
Last edited: