Pressurized containers: Stress distribution and large displacements

[Juanda]

TL;DR Summary

Two questions:
1) How is it possible to obtain the stress distribution without assuming it's constant along its thickness?
2) If the displacements are large, what would the equations look like?

I have a couple of questions about pressurized vessels. They're not completely related but since they're both about a similar topic I thought it'd be best to discuss them in a single thread. I'll be talking about a pressurized sphere (absolute internal pressure > 0 & absolute external pressure = 0) which I believe is the simplest case possible.

Question 1. Is it possible to obtain the stress distribution without assuming it's constant along its thickness?

Source: Mechanics of Materials by Barry J. Goodno and James M. Gere

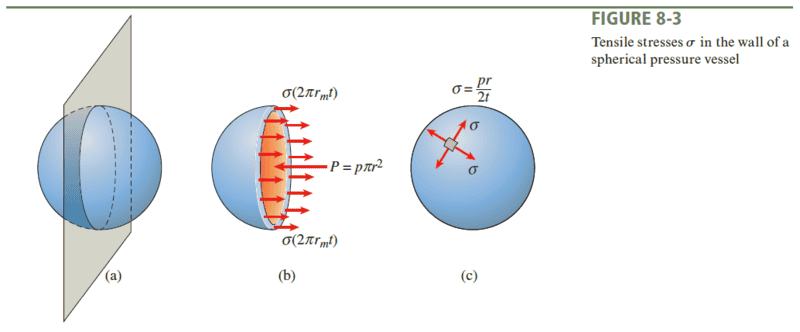
The book is clear in the derivation with $\sigma$ uniformly distributed across $t$ but I'm wondering how to derive the formulas without using that assumption.
Question 2. If the displacements are large, what would the equations look like? What is typically taught in undergrad courses is related to small displacements (maybe with the exception of buckling in columns with Euler's formula). In such cases, the displacements/deformations do not affect the reactions or the stresses.
However, if in this case with the pressurized sphere, the displacements are large, as the inner surface increases the net force on said surface will become greater too because the inner pressure is held constant (there'd be a pump for example). So there is constructive feedback that will cause a deformation greater than the predicted by the "typical" formula. I tried deriving the formula for the large displacement scenario using the "normal" case as the base but I can't reach anything useful. Besides, in the large displacement scenario, I assume it's necessary to account for the change in thickness as the sphere expands but then I get even more complex formulas I can't solve in any meaningful way.

 

[Chestermiller]

In question 1, if the only displacement is in the radial direction u(r), what are the three principal strains (in terms of u and r)?

 

[Juanda]

In question 1, if the only displacement is in the radial direction u(r), what are the three principal strains (in terms of u and r)?

Do you mean this? (This is the source by the way)

Then, to find the principal strains $\varepsilon_I$, $\varepsilon_{II}$ and $\varepsilon_{III}$ in terms of $u$ and $r$, I would have to diagonalize the strain tensor. However, since there will be no displacement in $z$ either in this case, the tensor is already diagonal so $\varepsilon_I=\frac{\partial u_r}{\partial r}$, $\varepsilon_{II}=\frac{u_r}{r}$, and $\varepsilon_{III}=0$ where I assumed $\frac{\partial u_r}{\partial r}>\frac{u_r}{r}$ which seems extremely likely in a scenario as the one being discussed.

 

[Chestermiller]

I’m asking for the strains in spherical coordinates, not cylindrical. The principal stresses and strains for this problem are in the three spherical coordinate directions.

 

[Juanda]

I’m asking for the strains in spherical coordinates, not cylindrical.

Oh. My bad.
I actually started the problem with a cylindrical container but then moved on to a spherical one because it appeared earlier in the book than the cylindrical case. I guess it's ordered like that because the extra symmetry simplified a few equations. It's late and my brain played me there.

Anyway, the point is that's indeed the information you're looking for. Just applied to a different case.
I believe this should be the equivalent equations for spherical coordinates applied to the simplified case where the displacements only happen in the radial direction. (This is the source)

Again, the tensor is already diagonal so $\varepsilon_I=\varepsilon_{rr}=\frac{\partial u_r}{\partial r}$ and $\varepsilon_{II}=\varepsilon_{III}=\varepsilon_{\theta \theta}=\varepsilon_{\varphi \varphi}=\frac{u_r}{r}$. That's also assuming $\frac{\partial u_r}{\partial r}>\frac{u_r}{r}$ as said in post #3.

Is that it?

 

[Chestermiller]

Oh. My bad.
I actually started the problem with a cylindrical container but then moved on to a spherical one because it appeared earlier in the book than the cylindrical case. I guess it's ordered like that because the extra symmetry simplified a few equations. It's late and my brain played me there.

Anyway, the point is that's indeed the information you're looking for. Just applied to a different case.
I believe this should be the equivalent equations for spherical coordinates applied to the simplified case where the displacements only happen in the radial direction. (This is the source)
View attachment 331192Again, the tensor is already diagonal so $\varepsilon_I=\varepsilon_{rr}=\frac{\partial u_r}{\partial r}$ and $\varepsilon_{II}=\varepsilon_{III}=\varepsilon_{\theta \theta}=\varepsilon_{\varphi \varphi}=\frac{u_r}{r}$. That's also assuming $\frac{\partial u_r}{\partial r}>\frac{u_r}{r}$ as said in post #3.

Is that it?

Yes indeed. Next questions:

Based on this, for a linear elastic Hookean solid, what are the three principal stresses in terms of these three strains, the Young's modulus, and the Poisson ratio?

What is the component of the stress equilibrium equation in the radial direction?

 

[Juanda]

I feel principal stresses and principal strains are connected with this equation although I couldn't find a reliable source to make sure of it.
$$
\begin{pmatrix}
\varepsilon_I\\\varepsilon_{II}
\\\varepsilon_{III}

\end{pmatrix}=\frac{1}{E}\begin{pmatrix}
1& -\nu & -\nu\\
-\nu& 1 &-\nu \\
-\nu& -\nu & 1
\end{pmatrix}\begin{pmatrix}
\sigma_{I}\\ \sigma_{II}
\\ \sigma_{III}

\end{pmatrix}
$$

I know that'd be true at least for the Cartesian case when there are no tangential stresses. I don't know if it can be used just like that in other coordinate systems now that we're talking about principal stresses and strains. Probably not but I couldn't find the relation between stress and strain in spherical coordinates for the moment.

I like where this is going but it's very late here so I'll have to leave it at this point for today. I'll try to keep going tomorrow after work. Thanks for the guidance so far.

 

[Chestermiller]

I feel principal stresses and principal strains are connected with this equation although I couldn't find a reliable source to make sure of it.
$$
\begin{pmatrix}
\varepsilon_I\\\varepsilon_{II}
\\\varepsilon_{III}

\end{pmatrix}=\frac{1}{E}\begin{pmatrix}
1& -\nu & -\nu\\
-\nu& 1 &-\nu \\
-\nu& -\nu & 1
\end{pmatrix}\begin{pmatrix}
\sigma_{I}\\ \sigma_{II}
\\ \sigma_{III}

\end{pmatrix}
$$

I know that'd be true at least for the Cartesian case when there are no tangential stresses. I don't know if it can be used just like that in other coordinate systems now that we're talking about principal stresses and strains. Probably not but I couldn't find the relation between stress and strain in spherical coordinates for the moment.

What I had in mind was the inverse of that:
$$\sigma_r=\frac{E}{(1+\nu)(1-2\nu)}[(1-\nu)\epsilon_r+\nu(\epsilon_{\theta}+\epsilon_{\phi})]$$$$\sigma_{\theta}=\frac{E}{(1+\nu)(1-2\nu)}[(1-\nu)\epsilon_{\theta}+\nu(\epsilon_{r}+\epsilon_{\phi})]$$$$\sigma_{\phi}=\frac{E}{(1+\nu)(1-2\nu)}[(1-\nu)\epsilon_{\phi}+\nu(\epsilon_{r}+\epsilon_{\theta})]$$

Stress equilibrium equation: $$\frac{d\sigma_r}{dr}+\frac{2\sigma_r-(\sigma_{\theta}+\sigma_{\phi})}{r}=0$$

Boundary Conditions:

$\sigma_r=0$ at $r = r_2$
$\sigma_r=-P$ at $r=r_1$

The strain-displacement equations, stress-strain equations, stress equilibrium equation, and these boundary conditions are sufficient to solve for the complete state of stress and strain as a function of radial location within the thick spherical shell.

 

[Juanda]

Stress equilibrium equation: $$\frac{d\sigma_r}{dr}+\frac{2\sigma_r-(\sigma_{\theta}+\sigma_{\phi})}{r}=0$$

Is this the origin of the stress equilibrium equation?

In this case, ignoring gravity so $\overline{g}=0$ and also with zero acceleration because it's in equilibrium so $\frac{\mathrm{d} \overline{v}}{\mathrm{d} t}=0$.

Boundary Conditions:

$\sigma_r=0$ at $r = r_2$
$\sigma_r=-P$ at $r=r_1$

The strain-displacement equations, stress-strain equations, stress equilibrium equation, and these boundary conditions are sufficient to solve for the complete state of stress and strain as a function of radial location within the thick spherical shell.

To recapitulate to make sure I'm following you. We know the acting pressures on the sphere. From that, we assumed a radial displacement field because it makes sense because of the mentioned acting pressure. We initially don't know the details of that displacement (how far each point goes, if every point moves the same amount, etc.) but we know for sure it's radial. From that piece of information, we'd simplify the equations because of the symmetries.

Lastly, in order to solve the equation you posted $\frac{d\sigma_r}{dr}+\frac{2\sigma_r-(\sigma_{\theta}+\sigma_{\phi})}{r}=0$. What can I do with $\sigma_{\theta}$ and $\sigma_{\phi}$? Do I just consider them constant? I don't feel like that's OK because they are dependent on the deformation and the expression from post #5 shows the deformation depends on the displacement field which also depends on $r$. So $\sigma_{\theta}$ and $\sigma_{\phi}$ are ultimately functions of $u_r$ which is a function of $r$.
I feel the only option is trying to write $\sigma_{r}$, $\sigma_{\theta}$ and $\sigma_{\phi}$ in terms of $u_r$. That would connect all the dots from the messages so far in this thread. I assume then I'll have a very long differential equation in terms of $\frac{\mathrm{d} u_r}{\mathrm{d} r}$ instead of $\frac{d\sigma_r}{dr}$. Is that how it's done?

 

[Chestermiller]

Is this the origin of the stress equilibrium equation?

View attachment 331293
In this case, ignoring gravity so $\overline{g}=0$ and also with zero acceleration because it's in equilibrium so $\frac{\mathrm{d} \overline{v}}{\mathrm{d} t}=0$.
To recapitulate to make sure I'm following you. We know the acting pressures on the sphere. From that, we assumed a radial displacement field because it makes sense because of the mentioned acting pressure. We initially don't know the details of that displacement (how far each point goes, if every point moves the same amount, etc.) but we know for sure it's radial. From that piece of information, we'd simplify the equations because of the symmetries.

Lastly, in order to solve the equation you posted $\frac{d\sigma_r}{dr}+\frac{2\sigma_r-(\sigma_{\theta}+\sigma_{\phi})}{r}=0$. What can I do with $\sigma_{\theta}$ and $\sigma_{\phi}$? Do I just consider them constant? I don't feel like that's OK because they are dependent on the deformation and the expression from post #5 shows the deformation depends on the displacement field which also depends on $r$. So $\sigma_{\theta}$ and $\sigma_{\phi}$ are ultimately functions of $u_r$ which is a function of $r$.
I feel the only option is trying to write $\sigma_{r}$, $\sigma_{\theta}$ and $\sigma_{\phi}$ in terms of $u_r$. That would connect all the dots from the messages so far in this thread. I assume then I'll have a very long differential equation in terms of $\frac{\mathrm{d} u_r}{\mathrm{d} r}$ instead of $\frac{d\sigma_r}{dr}$. Is that how it's done?

Yes, but it's not as complicated as you think or are expecting. When you go through all this algebra and calculus, you end up with a simple 2nd order ODE for u as a function of r. The analytic solution to this ODE is also very simple, involving 2 constants which are determined from the boundary conditions. Let's see what you obtain. I've already gone through this and gotten the final answer.

 

[Juanda]

Yes, but it's not as complicated as you think or are expecting. When you go through all this algebra and calculus, you end up with a simple 2nd order ODE for u as a function of r. The analytic solution to this ODE is also very simple, involving 2 constants which are determined from the boundary conditions. Let's see what you obtain. I've already gone through this and gotten the final answer.

Okay, maybe when I get to it I'll see things will simplify more than I expected because from my perspective I'm predicting a hellish experience of substitution after substation with a page-long equation.
Out of curiosity, did you do it with a computer or it's doable by hand? I mean, it's doable by hand for sure and people have done it before computers. But is it achievable by mere mortals?
I'm wondering if it's worth it to spend some time defining variables in the computer to do all the substitutions and simplifications or if it's better to just do it with pen and paper.

 

[Chestermiller]

Is this the origin of the stress equilibrium equation?

View attachment 331293
In this case, ignoring gravity so $\overline{g}=0$ and also with zero acceleration because it's in equilibrium so $\frac{\mathrm{d} \overline{v}}{\mathrm{d} t}=0$.

Yes. The divergence of the stress tensor is equal to zero; this is the stress equilibrium equation.

 

[Chestermiller]

Okay, maybe when I get to it I'll see things will simplify more than I expected because from my perspective I'm predicting a hellish experience of substitution after substation with a page-long equation.
Out of curiosity, did you do it with a computer or it's doable by hand? I mean, it's doable by hand for sure and people have done it before computers. But is it achievable by mere mortals?
I'm wondering if it's worth it to spend some time defining variables in the computer to do all the substitutions and simplifications or if it's better to just do it with pen and paper.

I'm guessing it took me about 20 minutes to get u(r) by hand. The ODE for u simplifies greatly, and does not even involve E or $\nu$. Later, I found my solution online. https://journals.sagepub.com/doi/full/10.1177/1464420719882958

 

[Juanda]

I'm guessing it took me about 20 minutes to get u(r) by hand. The ODE for u simplifies greatly, and does not even involve E or $\nu$. Later, I found my solution online. https://journals.sagepub.com/doi/full/10.1177/1464420719882958

Definitely, everything seems to be on the internet. I just must be awful at searching stuff.
I'll follow the process step by step. This kind of math is at the tip of my current capability so I can follow it if I focus a lot and reread it a few times but I can't derive it on my own.
Another day though. It's very late now and I need to rest.

 

[Juanda]

I'm guessing it took me about 20 minutes to get u(r) by hand. The ODE for u simplifies greatly, and does not even involve E or $\nu$. Later, I found my solution online. https://journals.sagepub.com/doi/full/10.1177/1464420719882958

That was a nice read. I had no idea about autofrettage. I knew about similar strategies used in reinforced concrete where the steel is in tension while the concrete is curing so that the concrete is pre-compressed to avoid tensional states. This being done in pressure vessels makes sense but I never knew it was an option.

Anyway, with some effort and thanks to the guidance from this thread I could follow the equations from the link you provided. After substituting, simplifying, solving, and simplifying again I now see what the tension in the body is:
$$\sigma_r=A-\frac{B}{r^3}$$
$$\sigma_{\theta}=\sigma_{\phi}=A+\frac{B}{2r^3}$$

After that, it makes sense to me why the book said "Furthermore since the wall is thin, you can assume with good accuracy that the stress is uniformly distributed across its thickness". If $r_{max} \approx r_{min}$ then the change in stress between the inner and outer shell will be very small too. It's kind of like how we consider gravity to be constant on the surface of Earth.

Question 1 from the OP is then solved.Now for question 2, it might not even make sense to think of it in terms of metals because the container would reap apart before the constructive feedback described in the OP has a chance to be noticeable but it'd be possible to derive some conclusion from the generalized version of Hooke's Law.
The original inspiration for the thread was this other post where flexible vinyl tubing is used in a water line (that's why I started thinking about the problem in terms of cylinders).

Let's then imagine that we're working with an ideal linearly elastic, isotropic material with low rigidity. Basically, I'm trying to understand how the equations would be if "The principle of relative stiffness" was not applied.

From Luis Ortega Berrocal - Resistencia de Materiales (Resistance of materials) - McGraw Hill

The principle of relative stiffness:
According to this principle, it's assumed that after applying an external force on the system its shape doesn't vary significantlly. Therefore, equilibrium conditions are imposed as if the deformed solid had the same shape and dimenions than before the deformation happened.

I already played around a little with this concept on this other thread but it led to a book from Timoshenko I could not follow because it is too dense and compact for me. These concepts are usually associated with torques that are amplified by the deformation of the body but when I realized this scenario with pressure vessels it felt very similar so if I could understand this maybe it would help me to connect the dots with the classical examples too.

 

[Chestermiller]

For the large displacement problem (question 2), we are still assuming thick wall, right? And we're still looking at the sphere problem?

 

[Juanda]

We can keep thinking about a sphere since it seems convenient with all the symmetries and now I'm familiar with it.

Regarding the thickness of the wall, I feel like the derivation should be independent of the thickness just like it was in "Question 1". Maybe once the results are obtained additional conclusion can be proposed such as "if the wall thickness is small compared with the average radius, the stress distribution can be assumed to be constant with reasonable accuracy".

However, I think it's convenient to first solve a simplification of problem 2 saying its thickness is small so the tension is constant along its thickness. I'd say it's reasonable to assume the constant tension in that scenario from the results obtained in problem 1. I'm convinced it must be possible to obtain the results without that assumption but I wouldn't even know where to start. On the other hand, I'm realizing just now that with what I learned so far when working on problem 1 I think I can give a new shot to problem two. I'll try to set up the differential equation and come back here.

 

[Juanda]

However, I think it's convenient to first solve a simplification of problem 2 saying its thickness is small so the tension is constant along its thickness. I'd say it's reasonable to assume the constant tension in that scenario from the results obtained in problem 1. I'm convinced it must be possible to obtain the results without that assumption but I wouldn't even know where to start. On the other hand, I'm realizing just now that with what I learned so far when working on problem 1 I think I can give a new shot to problem two. I'll try to set up the differential equation and come back here.

For a moment I thought I had it but no. I could make some progress setting up a differential equation to describe the problem but I'm missing information to solve it because I need more equations.

The orange area will grow as the body deforms. Its area will be:
$$S_r=\pi (r+dr)^2 = \pi (r^2+2rdr+dr^2) = \pi (r^2+2rdr)$$

The thickness of the circular crown in blue will change too.
$$S_R-S_r=\pi (R^2+2RdR-r^2-2rdr)$$

Then, the equilibrium of forces is:
$$(S_R-S_r)\sigma = S_rP_i \rightarrow (R^2+2RdR-r^2-2rdr)\sigma=(r^2-2rdr)P_i$$

Where I believe that $\sigma$ is $\sigma = \sigma_{\theta}=\sigma_{\phi}$. I also think the additional equations I need must come from the deformation-displacement fields but I don't know how to set that up for this given problem because I don't believe I can simply use the same as before.
Finally, I don't know how I'd solve this differential equation either. Maybe later on it'll simplify and become more manageable but right now it seems too hard for me.

 

[Chestermiller]

We can keep thinking about a sphere since it seems convenient with all the symmetries and now I'm familiar with it.

Regarding the thickness of the wall, I feel like the derivation should be independent of the thickness just like it was in "Question 1". Maybe once the results are obtained additional conclusion can be proposed such as "if the wall thickness is small compared with the average radius, the stress distribution can be assumed to be constant with reasonable accuracy".

What is your solution to problem 1 for the stresses as a function of P, r1, r2, and r only?

However, I think it's convenient to first solve a simplification of problem 2 saying its thickness is small so the tension is constant along its thickness. I'd say it's reasonable to assume the constant tension in that scenario from the results obtained in problem 1. I'm convinced it must be possible to obtain the results without that assumption but I wouldn't even know where to start. On the other hand, I'm realizing just now that with what I learned so far when working on problem 1 I think I can give a new shot to problem two. I'll try to set up the differential equation and come back here.

I'm not sure what you want to do in problem 2 with respect to assumptions. Also, maybe you want to reconsider and do the cylindrical problem as in your figure. Anyway, possible assumptions:

1. Small strains, linearized as a function of displacements

2. Plane stress (stress in thickness direction is negligible, and constant in-plane stresses across thickness)

3. Linear vs non-linear stress-strain behavior

 

[Juanda]

What is your solution to problem 1 for the stresses as a function of P, r1, r2, and r only?

For problem 1 I got what I needed to know. The derivation of the stress instead of just assuming it constant as the book suggested.
$$\sigma_r=A-\frac{B}{r^3}$$
$$\sigma_{\theta}=\sigma_{\phi}=A+\frac{B}{2r^3}$$
Then, using the initial conditions it's possible to obtain $A$ and $B$ in terms of $P$, $r_1$ and $r_2$.
$$\sigma_r(r_2)=0$$
$$\sigma_r(r_1)=-P$$
From that, it's possible to know the deformations and from the deformations, it's possible to know the displacement field so everything is solved and known.

I'm not sure what you want to do in problem 2 with respect to assumptions. Also, maybe you want to reconsider and do the cylindrical problem as in your figure. Anyway, possible assumptions:

1. Small strains, linearized as a function of displacements

2. Plane stress (stress in thickness direction is negligible, and constant in-plane stresses across thickness)

3. Linear vs non-linear stress-strain behavior

It seems we were both writing simultaneously. I should have posted #17 and #18 together but I got too excited while writing #17 because I thought I had the idea to solve it for a second so I sent the message to work on it. As you can read in #18 the idea that came to me was not enough... Reading #17 and #18 together might give you the context you're missing to better understand what I'm aiming at.
I'd like to at least know the stress in the sphere in this case with large deformation which is the key number to know if you want to guarantee your design won't break. Since it feels like there is a constructive feedback loop at play (more deformation → more force on the sphere → more deformation → etc.) I'd like to know the actual stress on the system.
Regarding the possible assumptions I'm initially considering constant stress in the radial direction (I don't know if that's equivalent to the plane stress you defined) and linear stress-strain behavior as shown in posts #17 and #18.
However, I'm stuck and I don't know where to find more equations to solve the variables I obtained in #18 after applying the equilibrium of forces once the body is deformed. I assume it's necessary to link them with the strain and displacement fields but I'm not sure how.
I guess it's OK to reuse the expression for stress-strain just like in Question 1 because I'm also assuming it's linear.
But for the displacements, I don't know if I can reuse it as well to try to solve it. I feel that expression is derived from the assumption of small displacements which is no longer the case in Question 2.

 

[Chestermiller]

I'm having trouble understanding what you are trying to do in problem 2.

 

[Chestermiller]

With large displacements and strains, you would write $$r=r(\bar{r})$$where $\bar{r}$ is the location of a material point at P=0 and r is the location of the same material point at pressure P inside. So the amount of stretching in the radial direction is $$\lambda_r=\frac{dr}{d\bar{r}}$$ and the amount of stretching in the in-plane directions is $$\lambda_{\theta}=\lambda_{\phi}=\frac{r}{\bar{r}}$$We would also be expressing the stress-equilibrium equation in terms of the material coordinate $\bar{r}$ as the independent variable: $$\frac{d\sigma_r}{\lambda_rd\bar{r}}+\frac{2\sigma_r-\sigma_{\theta}-\sigma_{\phi}}{\bar{r}\lambda_{\theta}}=0$$Unfortunately, for large deformations, the stresses are not linear functions of the strains, and, to make matters worse, there are multiple strain measures (determined by the two stretch ratios), all of which reduce to the same strains in the limit of small displacements. It is not known which strain measure would give the most concise results for the two stresses.

 

[Juanda]

I'm having trouble understanding what you are trying to do in problem 2.

Yeah. I'm not explaining myself very well here. Let me give it another go.

I suspect there exists a feedback loop with pressurized tanks when the inner pressure is kept constant (more deformation → more force on the sphere because of the increased surface and constant pressure → more deformation → etc.).

This is somewhat similar to a problem like the one shown in the following picture.

Typically, equilibrium and deformations are considered to be independent because displacements are considered small (principle of relative stiffness). Therefore, usually, we'd say the reaction at the base is simply $FL$.
However, if we allow for the displacements to be large, the equilibrium after the deformation will be different and the reactions larger. In this example, if we take into account the displacement due to the external load, which would offer a more accurate solution, the moment at the base would be $FL'$ which is larger than $FL$. Of course, if the displacements are small, both results are basically the same so there is not much added value to bother with the extra complexity because finding $L'$ is no easy task (that's the kind of thing I was trying to find out how to do with this post I mentioned earlier).

Now, for the case of the pressurized vessel in question 2. I'd say it's OK to start working on the simpler version of the problem where the thickness is small enough to consider the tension to be constant in the radial direction. This is a reasonable assumption derived from the results obtained in question 1.
If the equilibrium of forces is not linked to the deformation, the book provides an easy derivation of the tension. (Note: I'll be using $r$ for the inner radius, $R$ for the outer radius and $P_i$ for the inner pressure.)

The force to the left done by the inner pressurized gas must be the same as the force to the right done by the tension in the shell. Again, since we're saying equilibrium is applied to the undeformed geometry, the equation looks like this.
$$P_i (\pi r^2)=\sigma (\pi(R^2-r^2)) \rightarrow \sigma = \frac{P_i (\pi r^2)}{\pi(R^2-r^2)}$$

From that, it's possible to obtain the stress in all directions which is enough to apply Von Misses and find out if it will resist or not.

However, if we input the change in geometry due to the deformation into the equilibrium equation, the resulting equality is much harder. First, it is necessary to compute the change in geometry. The orange surface will grow in an amount $dr$ and the blue crown will change depending on $dR$ and $dr$. Then, the surfaces after the deformation will be:
The orange surface where the gas acts:
$$S_r=\pi (r+dr)^2 = \pi (r^2+2rdr+dr^2) = \pi (r^2+2rdr)$$
The blue surface where the tension of the shell acts:
$$S_R-S_r=\pi (R^2+2RdR-r^2-2rdr)$$
Finally, the equilibrium of forces will be:
$$(S_R-S_r)\sigma = S_rP_i \rightarrow (R^2+2RdR-r^2-2rdr)\sigma=(r^2-2rdr)P_i$$
When the deformations and the equilibrium of forces were unlinked, it was possible to just solve the equation and find the stress but now it's just not possible. It's necessary to add some extra information which I believe must come from the displacement field but I don't know how to do it. I think knowing the value of $\sigma$ calculated like that is relevant because, as shown for the case with the moment $FL'$, the resulting $\sigma$ from this procedure will be greater than the one obtained before. Regarding the strain, I feel it'd be perfectly OK for it to behave linearly since that's just a property of the material. But the displacement field will not be linear for sure. Or that's what I think. I have no way to prove anything yet.

With large displacements and strains, you would write $$r=r(\bar{r})$$where $\bar{r}$ is the location of a material point at P=0 and r is the location of the same material point at pressure P inside. So the amount of stretching in the radial direction is $$\lambda_r=\frac{dr}{d\bar{r}}$$ and the amount of stretching in the in-plane directions is $$\lambda_{\theta}=\lambda_{\phi}=\frac{r}{\bar{r}}$$We would also be expressing the stress-equilibrium equation in terms of the material coordinate $\bar{r}$ as the independent variable: $$\frac{d\sigma_r}{\lambda_rd\bar{r}}+\frac{2\sigma_r-\sigma_{\theta}-\sigma_{\phi}}{\bar{r}\lambda_{\theta}}=0$$Unfortunately, for large deformations, the stresses are not linear functions of the strains, and, to make matters worse, there are multiple strain measures (determined by the two stretch ratios), all of which reduce to the same strains in the limit of small displacements. It is not known which strain measure would give the most concise results for the two stresses.

This could be the extra information I need but I can't see how to relate it to the equation of equilibrium I posted. I find the last part especially disturbing. Are you saying there are two solutions and we have no way of knowing which one is the correct one?

 

[Chestermiller]

You're talking about doing a balloon, and determining how much bigger the balloon gets as we increase the pressure. The in-plane stretch ratio is $$\lambda_{\theta}=r/r_0$$ where $r_0$ is the radius when the pressure is small enough (negligibly above atmospheric) just to establish the initial spherical shape. If the rubber is incompressible, we have $$\lambda_r\lambda_{\theta}^2=1$$. So, if the initial thickness of the membrane is $t_0$, the thickness when the balloon is inflated is $$t=\frac{t_0}{\lambda_{\theta}^2}$$At pressure P, we have $$\sigma(\lambda_{\theta})=\frac{Pr}{2t}=\frac{Pr_0}{2t_0}\lambda_{\theta}^3$$or $$\frac{\sigma(\lambda_{\theta})}{\lambda_{\theta}^3}=\frac{Pr_0}{2t_0}$$If we knew the functional relation between the stress $\sigma$ and $\lambda_{\theta}$, we could determine the balloon radius as a function of the imposed pressure P.

The desired relationship can be determined by independent laboratory experiments involving biaxial stretching a flat sheet of the rubber, and measuring the force F on the edge of the sample as a function of the stretch ratio $\lambda$: $$F=\sigma tL=\sigma t_0 L_0\frac{t}{t_0}\frac{L}{L_0}$$or$$\sigma=\frac{F}{t_0 L_0}\lambda$$So the experiment involves measuring F as a function of L in a biaxial stretching experiment, calculating the stress as a function of the stretch ratio, then plotting $\sigma/\lambda^3$ vs $\lambda$.

 

[Juanda]

You're talking about doing a balloon, and determining how much bigger the balloon gets as we increase the pressure. The in-plane stretch ratio is $$\lambda_{\theta}=r/r_0$$ where $r_0$ is the radius when the pressure is small enough (negligibly above atmospheric) just to establish the initial spherical shape.

You're right. At that point ballon would be more appriate than tank.
Still, I think I can see the similarities in deformation when compared with expressions previously shared in the thread like:
$$\varepsilon_\theta=\frac{u_r}{r}$$
Which looks a lot like the expression of $\lambda_\theta$ you showed. I assume then that $\lambda_\theta=\lambda_\phi$ just like it happened with the tank before.

If the rubber is incompressible, we have $$\lambda_r\lambda_{\theta}^2=1$$.

I did some digging but I couldn't figure this out. I'm guessing the expression $\lambda_r\lambda_{\theta}^2=1$ comes from saying $\lambda_r\lambda_{\theta}\lambda_{\phi}=1$ but I don't know why that's true.
I tried to reach that result using a simple case. I imagined an incompressible rod in uniaxial tension and doing
$\varepsilon_{I}\varepsilon_{II}\varepsilon_{III}$ but I didn't get $1$ as the result.
Uniaxial tension → $\sigma_{I} \neq 0$; $\sigma_{II} = \sigma_{III}= 0$
Incrompressible → $v=0.5$
Expressions for $\varepsilon_{I}$; $\varepsilon_{I}$ and $\varepsilon_{III}$ from generalized Hooke's Law (posted in #7)

$$
\begin{pmatrix}
\varepsilon_I\\\varepsilon_{II}
\\\varepsilon_{III}

\end{pmatrix}=\frac{1}{E}\begin{pmatrix}
1& -\nu & -\nu\\
-\nu& 1 &-\nu \\
-\nu& -\nu & 1
\end{pmatrix}\begin{pmatrix}
\sigma_{I}\\ \sigma_{II}
\\ \sigma_{III}

\end{pmatrix}
$$

Then, if I multiply $\varepsilon_{I}\varepsilon_{II}\varepsilon_{III}$ following my guess what I get is:
$$\varepsilon_{I}\varepsilon_{II}\varepsilon_{III}=\frac{\sigma_I^3}{4E^3}$$ which I don't see how or why it could be one. Is $\varepsilon_{I}\varepsilon_{II}\varepsilon_{III}=1$ only because of the spherical deformation?

I got blocked there and I feel I need to understand it to be able to continue with the rest.

 

[Chestermiller]

You're right. At that point ballon would be more appriate than tank.
Still, I think I can see the similarities in deformation when compared with expressions previously shared in the thread like:
$$\varepsilon_\theta=\frac{u_r}{r}$$
Which looks a lot like the expression of $\lambda_\theta$ you showed. I assume then that $\lambda_\theta=\lambda_\phi$ just like it happened with the tank before.

$$\lambda_r=1+\frac{du}{dr}$$
$$\lambda_{\theta}=\lambda_{\phi}=1+\frac{u}{r}$$

I did some digging but I couldn't figure this out. I'm guessing the expression $\lambda_r\lambda_{\theta}^2=1$ comes from saying $\lambda_r\lambda_{\theta}\lambda_{\phi}=1$ but I don't know why that's true.

That is the condition for incompressibility. It just says that volume is constant.

I tried to reach that result using a simple case. I imagined an incompressible rod in uniaxial tension and doing
$\varepsilon_{I}\varepsilon_{II}\varepsilon_{III}$ but I didn't get $1$ as the result.
Uniaxial tension → $\sigma_{I} \neq 0$; $\sigma_{II} = \sigma_{III}= 0$
Incrompressible → $v=0.5$
Expressions for $\varepsilon_{I}$; $\varepsilon_{I}$ and $\varepsilon_{III}$ from generalized Hooke's Law (posted in #7)

Then, if I multiply $\varepsilon_{I}\varepsilon_{II}\varepsilon_{III}$ following my guess what I get is:
$$\varepsilon_{I}\varepsilon_{II}\varepsilon_{III}=\frac{\sigma_I^3}{4E^3}$$ which I don't see how or why it could be one. Is $\varepsilon_{I}\varepsilon_{II}\varepsilon_{III}=1$ only because of the spherical deformation?

For infinitesimal strains, the condition of incompressibility becomes $$\epsilon_1+\epsilon_2+\epsilon_3=0$$This neglects products of the strains as being negligible.

 

[Juanda]

$$\lambda_r=1+\frac{du}{dr}$$
$$\lambda_{\theta}=\lambda_{\phi}=1+\frac{u}{r}$$

Hmmmm. Is the $1$ a typo? It's the only thing that makes it different from the previous expressions. Not only when compared with the expressions for the tank but also the expression for the balloon you shared in previous posts.
A few times during the thread we've changed the letters so I'm not sure if these are new variables or if it's a small typo.

That is the condition for incompressibility. It just says that volume is constant.

For infinitesimal strains, the condition of incompressibility becomes $$\epsilon_1+\epsilon_2+\epsilon_3=0$$This neglects products of the strains as being negligible.

I can see why when saying incompressible immediately the result must be $\epsilon_1+\epsilon_2+\epsilon_3=0$. Whatever direction grows must make others diminish so the sum is 0.
I checked the uniaxial tension case with $v=0.5$ and indeed the result is 0.
But, how is that related with $\epsilon_1\epsilon_2\epsilon_3=1$? If those 3 values tend to 0 I'd expect the product to be 0 as well instead of 1.
Besides, you're calling for infinitesimal strains. I'd have thought the main point from question two is to work with big strains. If they're small strains, then it'd be possible to solve it in the same way as question 1, wouldn't it?

 

[Chestermiller]

Hmmmm. Is the $1$ a typo?

The 1 is correct. I hope you understand the difference between stretch ratio and strain.

It's the only thing that makes it different from the previous expressions. Not only when compared with the expressions for the tank but also the expression for the balloon you shared in previous posts.
A few times during the thread we've changed the letters so I'm not sure if these are new variables or if it's a small typo.I can see why when saying incompressible immediately the result must be $\epsilon_1+\epsilon_2+\epsilon_3=0$. Whatever direction grows must make others diminish so the sum is 0.
I checked the uniaxial tension case with $v=0.5$ and indeed the result is 0.

But, how is that related with $\epsilon_1\epsilon_2\epsilon_3=1$? If those 3 values tend to 0 I'd expect the product to be 0 as well instead of 1.

The product of the 3 stretch ratios is equal to 1, not the product of the 3 strains. The sum of the 3 principal infinitesimal strains is equal to 0 (for incompressibility).

Besides, you're calling for infinitesimal strains. I'd have thought the main point from question two is to work with big strains. If they're small strains, then it'd be possible to solve it in the same way as question 1, wouldn't it?

There are several different definitions of strain in the case of large deformations. They all reduce to the same equations for infinitesimal strains, but they are all different for larger strains.. So which one do you use? On the other hand, the stretch ratios are always the same. We are solving the balloon problem for large deformations. However, the relation between stress and stretch ratio is no longer known in advance using, say, the Hooke's law equations. In the balloon problem, all we know is that the stress is a non-linear function of the stretch ratio, which has to be measured in the laboratory in a separate experiment. One example of a finite strain definition (out of the many) is $$\epsilon=\frac{\lambda^2-1}{2}$$So, for our balloon case, we would have $$\epsilon_{\theta}=\frac{u}{r_0}-\frac{1}{2}\left(\frac{u}{r_0}\right)^2$$where $u=r-r_0$.

 

[Chestermiller]

To analyze large deformation behavior, a material coordinate system is always used. The material coordinate system acts as a permanent label for each particle of material comprising the body. Let $x_0$, $y_0$, and $z_0$ be the coordinates of a particle of material within the body in the undeformed configuration of the body. Let x, y, z be the coordinates of the same particle of material in the deformed configuration of the body. Then, the relationship between undeformed and deformed coordinates are defined by the mapping functions $x=x(x_0,y_0,z_0)$, $y=y(x_0,y_0,z_0)$, and $z=z(x_0,y_0,z_0)$.

If $z_0+dz_0$, $y_0+dy_0$, $z_0+dz_0$ are the material coordinates of a closely neighboring material point in the undeformed configuration of the body, how are the differential changes in the coordinates dx, dy, and dz between the same pair of material points in the deformed configuration of the body related?

 

[Juanda]

The 1 is correct. I hope you understand the difference between stretch ratio and strain.

To be honest I don't remember being taught about stretch ratios while I was in university. It might be a language issue. It's not that I don't understand it. I checked the formula and I know what it is.
Simply I think we don't have a specific word to define that. It could also be I simply don't remember the name though. We just used forces, stress, strain, and displacements. I actually don't see much added value in incorporating the stretch ratio into the mix of variables that already seem to fully define the situation but my conception might change as I learn more.
In fact, I thought you swapped from $\epsilon$ to $\lambda$ to indicate we're tackling question 2 about the balloon instead of question 1 about the tank.

The product of the 3 stretch ratios is equal to 1, not the product of the 3 strains. The sum of the 3 principal infinitesimal strains is equal to 0 (for incompressibility).

Yeah, after noticing the difference between strain and stretch ratio I see how it makes sense.

There are several different definitions of strain in the case of large deformations. They all reduce to the same equations for infinitesimal strains, but they are all different for larger strains.. So which one do you use? On the other hand, the stretch ratios are always the same.

I guess that'd be a reason to try using stress ratio instead of strain.

If $z_0+dz_0$, $y_0+dy_0$, $z_0+dz_0$ are the material coordinates of a closely neighboring material point in the undeformed configuration of the body, how are the differential changes in the coordinates dx, dy, and dz between the same pair of material points in the deformed configuration of the body related?

Wouldn't I need to know the functions for $x$; $y$; $z$ to be able to answer that question?
For example,
$$x=x_0+1$$
So every point moves 1 unit to the right. Now I can check where that neighboring point you described would end up by inputting that into the previous expression.
$$x=x_0+dx_0+1$$
Is that what you meant with your question?

 

[Chestermiller]

To be honest I don't remember being taught about stretch ratios while I was in university. It might be a language issue. It's not that I don't understand it. I checked the formula and I know what it is.
Simply I think we don't have a specific word to define that. It could also be I simply don't remember the name though. We just used forces, stress, strain, and displacements. I actually don't see much added value in incorporating the stretch ratio into the mix of variables that already seem to fully define the situation but my conception might change as I learn more.
In fact, I thought you swapped from $\epsilon$ to $\lambda$ to indicate we're tackling question 2 about the balloon instead of question 1 about the tank.Yeah, after noticing the difference between strain and stretch ratio I see how it makes sense.I guess that'd be a reason to try using stress ratio instead of strain.

For large deformation situations, the stretch ratio is not ambiguous,, but the strain is.

Wouldn't I need to know the functions for $x$; $y$; $z$ to be able to answer that question?
For example,
$$x=x_0+1$$
So every point moves 1 unit to the right. Now I can check where that neighboring point you described would end up by inputting that into the previous expression.
$$x=x_0+dx_0+1$$
Is that what you meant with your question?

No. I already specified the functionality: $x=x(x_0,y_0,z_0)$, same for y and z. So, $$dx=\frac{\partial x}{\partial x_0}dx_0+\frac{\partial x}{\partial y_0}dy_0+\frac{\partial x}{\partial z_0}dz_0$$same for dy and dz.

Let $(ds)^2$ be the square of distance between the two closely neighboring material points in the deformed configuration of the body. Please express $(ds)^2$ in terms of $dx_0, \ dy_0,\ and\ dz_0$ (not dx, dy and dz). That is, in terms of the differential differences of the coordinates of the two material points in the undeformed configuration of the body.

 

[Juanda]

I'm trying to visualize what you're asking for. Let me drop the $z$ component so that's simpler to draw.
We have the points $A$ and $B$.
Before the deformation, their positions are $A_0$ and $B_0$ and after the deformation, they are $A$ and $B$. After the deformation, they are very close.

From the diagram, I can express $ds$ in terms of $A$ and $B$ but that will result in an expression dependent of $dx$ and $dy$.
$$\left \| d\vec{s} \right \|^2 = \left \| \vec{B}-\vec{A} \right \|^2=\left \| (dx,dy) \right \|^2=dx^2+dy^2$$
Where $dx$ and $dy$ can be obtained from what you shared:
$$dx=\frac{\partial x}{\partial x_0}dx_0+\frac{\partial x}{\partial y_0}dy_0$$

I doubt that's the expression of $\left \| d\vec{s} \right \|^2$ you're looking for because there still are $\partial x$ in it.
I'm not sure I'm prepared to understand question 2.
I'm already thankful for at least being able to follow you through question 1 (the tank with small deformations without assuming constant stress in the shell) but question 2 (the balloon with big deformations) seems orders of magnitude more complex.
It's not my intention to waste your time so if I'm still far off what're trying to transmit I think it'll be better if I just keep reading books before trying to tackle something like this.

 

[Juanda]

It's not my intention to waste your time so if I'm still far off what're trying to transmit I think it'll be better if I just keep reading books before trying to tackle something like this.

I'm answering just to make sure the message goes through as I understand it.
When I say "far off" I don't mean that there's still a lot to go. I can keep going without issues.
What I was trying to say is that if you realize I just lack a strong enough base to understand this now then I won't waste more of your time and I'll focus on easier problems before trying to deal with something like this for which I'm not yet ready.

 

[Chestermiller]

I'm trying to visualize what you're asking for. Let me drop the $z$ component so that's simpler to draw.
We have the points $A$ and $B$.
Before the deformation, their positions are $A_0$ and $B_0$ and after the deformation, they are $A$ and $B$. After the deformation, they are very close.
View attachment 331716

From the diagram, I can express $ds$ in terms of $A$ and $B$ but that will result in an expression dependent of $dx$ and $dy$.
$$\left \| d\vec{s} \right \|^2 = \left \| \vec{B}-\vec{A} \right \|^2=\left \| (dx,dy) \right \|^2=dx^2+dy^2$$
Where $dx$ and $dy$ can be obtained from what you shared:
$$dx=\frac{\partial x}{\partial x_0}dx_0+\frac{\partial x}{\partial y_0}dy_0$$

I doubt that's the expression of $\left \| d\vec{s} \right \|^2$ you're looking for because there still are $\partial x$ in it.

You've done it correctly so far. In a given problem, we usually don't know the relationship between dx etc. and $dx_0$ etc. yet. That's what you are solving for. So, please substitute our equations for dx and dy in terms of $$dx_0\ and\ dy_0$$ into your equation for $(ds)^2$ and express the result in the form $$(ds)^2=A(dx_0)^2+B(dy_0)^2+Cdx_0dy_0$$. What do you get for A, B, and C?

I'm not sure I'm prepared to understand question 2.
I'm already thankful for at least being able to follow you through question 1 (the tank with small deformations without assuming constant stress in the shell) but question 2 (the balloon with big deformations) seems orders of magnitude more complex.
It's not my intention to waste your time so if I'm still far off what're trying to transmit I think it'll be better if I just keep reading books before trying to tackle something like this.

Well, I'm trying to lead you through how we would approach large deformation mechanics. The first step is to establish the displacement-strain equations for large displacements.

 

[Chestermiller]

I'm answering just to make sure the message goes through as I understand it.
When I say "far off" I don't mean that there's still a lot to go. I can keep going without issues.
What I was trying to say is that if you realize I just lack a strong enough base to understand this now then I won't waste more of your time and I'll focus on easier problems before trying to deal with something like this for which I'm not yet ready.

I understand. Even linear strains and displacements together with linear relation for the stress tensor isn't that easy. You need to at least have some familiarity with 2nd order tensors and how to apply them. For large displacements and strains, things are much more complicated. Try Googling "large displacement mechanics" or "large displacement mechanics." Or hit the Continuum Mechanics literature.