Rowing a Boat Across a River - FODE Physics Problem

[Athenian]

Homework Statement

A boater rows across a straight river of constant width $w$, always heading (i.e., pointing the front of the boat) toward the position on the bank directly opposite the starting point. If the river flows with uniform speed $v$ and if the speed with which the boater can row is also $v$, find the equation of the path of the boat. How far downstream does the boater finally land? [Hint: if $x$ is the cross-stream position of the boat and $y$ is its downstream position, find an expression for $dy/dx$. Then solve for $y(x)$.]

Afterward, please find the trajectory of the boat ($x$ vs. $y$ or $y$ vs. $x$) upon deriving the differential equation.

Relevant Equations

Refer Below $\longrightarrow$

First off, to solve for this problem, I relied largely on my below drawn diagram. Forgive the poor work as this was done on a laptop.

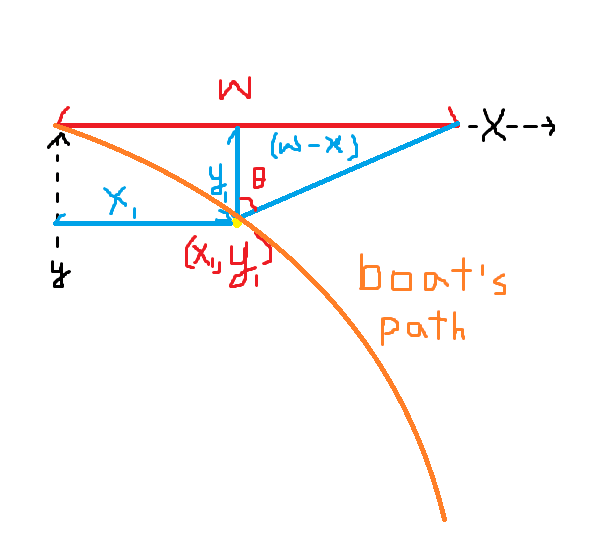
Using the above image as reference, I came up with the below equations.

$$\frac{dy}{dx} = \frac{sin \, \theta}{1- cos \, \theta}$$

where $cos \, \theta = \frac{y}{\sqrt{(w-x)^2 + y^2}}$ and $sin \, \theta = \frac{w-x}{\sqrt{(w-x)^2 + y^2}}$.

Substituting the original value of $sin \, \theta$ and $cos \, \theta$ back into the first written equation, I get:

$$\frac{dy}{dx} = \frac{w-x}{\sqrt{(w-x)^2 +y^2} -y}$$

Despite my best efforts to create a separable equation and ultimately solve for $y$ (i.e. the downstream distance the boat traveled altogether), I had an incredibly difficult time doing so.

After searching online, I did come across to this site where another user from ten years ago had nearly the same solution as I do (https://www.physicsforums.com/threads/row-boat-fode.379923/). However, this user did make an interesting substitution as seen below:

$$z = w- x$$
$$dz = -dx$$

From there, we can take those values and plug it back in where we last left off:
$$- \frac{dy}{dz} = \frac{z}{\sqrt{z^2 +y^2} - y}$$
$$\Rightarrow dy = \frac{-zdz}{\sqrt{z^2 +y^2} - y}$$

Despite having this simpler expression, though, I am still having a hard time solving for $y$. Any help and guidance regarding my question here would be greatly appreciated. Thank you very much for reading through my question!

 

[BvU]

Hi,

$$\frac{dy}{dx} = \frac{sin \, \theta}{1- cos \, \theta} $$

How did you derive that ? Your $\theta$ starts out at $\pi/2$ and gradually diminishes to $0$.

What do you have for the velocities ?

Then from $dy = v_y dt$ and $dx = v_x dt\ ,\ \$ you get $\displaystyle {dy\over dx}$

 

[Athenian]

@BvU , thank you so much for the reply!

Admittingly, my derivation of $\frac{dy}{dx} = \frac{sin \, \theta}{1- cos \, \theta}$ is based mostly out of "intuition" (if I could call it that).

Essentially, I reasoned that when the boat is just about to travel across the stream, the slope of the boat's path would be $1$ since both the boat is traveling at a speed of $v$ in the x-direction while the stream is traveling at that same speed in the $y$ direction.

Once the boat arrives at its destination, though, the boat will be pointing completely in the y-direction. In other words, to put my statement in a graph, it would essentially be an asymptote. Thus, to fulfill both these requirements of having a slope of $1$ in the beginning and having a slope of $\infty$ (or error) at the destination, I came up with $\frac{dy}{dx} =\frac{sin \, \theta}{1- cos \, \theta}$. I suppose the fact that students in the same course seemingly reconfirmed my answer made me more confident in the solution.

Needless to say, the above approach should not be "correct". Therefore, per your instructions, I did go ahead and try to find for $dy/dx$ the correct way. Note that I am not 100% certain whether $\frac{dy}{dx} =\frac{sin \, \theta}{1- cos \, \theta}$ is technically correct or not.

Considering that $v_x = \frac{dx}{dt}$ and $v_y = \frac{dy}{dt}$ are components of $v = \frac{dr}{dt}$, I came up with the below equation:

$$\frac{dy}{dx} = \frac{\Big( v \, sin \, \theta \Big) dt}{\Big( v \, cos \, \theta \Big) dt}$$

First off, I am not even sure am I supposed to be approaching finding for $v_x$ and $v_y$ this way. However, assuming that my approach for the above equation is correct, how do I even simplify that?

Perhaps it's just me, but I feel like my thought process toward getting the algebraic expression for the velocity components is incorrect.

Any help would be greatly appreciated. Once again, thank you for your reply!

 

[BvU]

Essentially, I reasoned that when the boat is just about to travel across the stream, the slope of the boat's path would be $1$ since both the boat is traveling at a speed of $v$ in the $x$-direction while the stream is traveling at that same speed in the $y$-direction.

Agreed. But not very helpful, since an inverse would satisfy the same condition .

Once the boat arrives at its destination, though, the boat will be pointing completely in the $y$-direction. In other words, to put my statement in a graph, it would essentially be an asymptote.

That is kind of jumping to a conclusion. Yes, the boat will point completely in the $y$ direction. But no, $y$ at that point does not change any more (nor does $x$). That is not a characteristic of an asymptote, but of a stationary point: in practice the journey comes to an end when one of the oars can't be lowered into the water any more. We need not be concerned about that kind of detail and just have to find the trajectory of the boat.

I suppose the fact that students in the same course seemingly reconfirmed my answer

The internet is notoriously unreliable ( and PF is on the internet )

For $v_y$ you write $v\sin\theta$ but the picture clearly shows that should be a cosine. And you omit the contribution from the river flowing (our coordinate system is land-based, isn't it ?) .

I am not even sure am I supposed to be approaching finding for $v_x$ and $v_y$ this way

Admittedly, physicists are very casual about infinitesimals. One should take limits and distinguish pathologic exceptions etcetera, but usually one can bluntly simplify as if it were simple algebra, so:$$\frac{dy}{dx} = \frac{\Big( v \, sin \, \theta \Big) dt}{\Big( v \, cos \, \theta \Big) dt}\ \ \Rightarrow \quad \frac{dy}{dx}=\tan\theta$$ (which, for reasons indicated above, is not the right equation ).

Look again at your sketch and see if you can find a sensible $\frac{dy}{dx}$ that you can convince yourself is correct.

Also look at the approach to $\theta = 0$ at the end and see $\lim {dy\over dx}\ne\infty$. In other words: your curve isn't correct !
Which can be understood if you consider that an ever bigger fraction of $v$ from the river is counteracted when $\theta\downarrow 0$.

Note:
If no one proves me wrong, we will have to exhume the old thread and put things right there ! But I'm right - he said confidently .

 

[Athenian]

Wow, this was an incredibly informative explanation, @BvU . I really appreciate the effort gone into this to help me better understand what's going on with the physics and math for this question.

Anyway, below is my solution upon fixing some mistakes in my previous post as well as following according to your hints and guidelines.

Starting with correcting the obvious mistake :
$$v_y = v \, cos \, \theta$$
$$v_x = v \, sin \, \theta$$

The above represents the velocity components of the boat. But, as you have mentioned, I have neglected the speed of the river which can be represented as $v_y = v \, cos \, (0)$ since it is following in one (downward) direction at $\theta = 0$.

With this information, I can construct the following equation:
$$\frac{dy}{dx} = \frac{(v \, cos \, \theta - v \, cos(0)) dt}{(v \, sin \, \theta)dt}$$
$$\Rightarrow \frac{v \, cos \, \theta - v \, cos(0)}{v \, sin \, \theta}$$
$$\Rightarrow \frac{v (cos \, \theta - cos(0))}{v \, sin \, \theta}$$
$$\Rightarrow \frac{cos \, \theta -1}{sin \, \theta}$$

I should also note that (as a personal review) the minus sign in the denominator is there simply because as the boat is traveling toward its destination, it is speeding against the river's downstream current.

As a bonus, I did graph out my equation on Wolfram|Alpha and it looks correct in my opinion. Please let me know what you think about my attempted solution. Thank you so much for your assistance!

Assuming my solution thus far is correct, I decided to continue on with the problem. Plugging in the values quoted below:

$cos \, \theta = \frac{y}{\sqrt{(w-x)^2 + y^2}}$ and $sin \, \theta = \frac{w-x}{\sqrt{(w-x)^2 + y^2}}$.

I can get:
$$\frac{dy}{dx} = \frac{y- \sqrt{y^2 + (w-x)^2}}{w-x}$$

Next, my goal is to find the algebraic value for $y$ in order to determine "[h]ow far downstream does the boater finally land".

But, here's where my issue comes in. I just can't solve for $y$. I did try what I attempted to do in my initial post where I substituted $w-x$ for one arbitrary value of $z$. To accommodate the change, I also likewise made $dz = -dx$. But, after spending some time thinking about it, I am harboring doubts for this solution method provided by the same user which I provided the URL for in my initial post.

In short, what would be the best, most efficient, and straightforward way to find $y$?

Once again, thank you so much for your kind assistance. This has been both incredibly insightful and helpful!

Side Note: Assuming my equation for $dy/dx$ is correct, I think I can safely say that you can "exhume the old thread and put things right there". :)

 

[BvU]

Assuming my solution thus far is correct

Not convinced yet ?

I just can't solve for $y$.

Tell you a secret: I can't either. I'm notoriously bad at differential equations. Cause is the availability of numerical solvers in combination with my laziness. So the temptation to skip the analytical attempt always wins .

I cheated two ways: Euler integration in excel and wolframalpha. try entering
dy/dx = (sqrt((1-x)^2+y^2)-y)/(1-x),y(0)=0
there and be surprised by the simple analytical solution !

(I had the river flowing in y+ direction)

 

[Athenian]

Haha. I'm convinced now upon overcoming my overly-cautious tendencies.

Hmmm, admittingly, my professor has yet to go through Euler integration yet. But, thanks for providing the Wolfram|Alpha link as well as the "simply analytical solution". Nonetheless, I still need to figure out how to go about solving this messy equation step-by-step by using first-order differential equation methods ...
Well, I'll see what I can do. However, if anybody could provide a hint, I would greatly appreciate it!

Once again, thank you for all your help, BvU!

 

[haruspex]

$$\frac{dy}{dx} = \frac{y- \sqrt{y^2 + (w-x)^2}}{w-x}$$

Switching x around, i.e. replacing x with w-x, that reduces to $xy'^2+2yy'=x$
Reinstating theta as atan(y/x), I get $(x\theta'+\sin(2\theta))^2=\cos^2(\theta)$, whence $x\theta'+\sin(2\theta)=\pm\cos(\theta)$.
From there you can proceed to integration.

I end up with $x^6=w^6(1+s)^3(1-s)(1+2s)^{-4}$, where $s=\sin(\theta)$ and initially x=w, s=0.
With a spreadsheet, I verified this matches the ODE.

 

[Athenian]

Thank you very much for the help. This was incredibly insightful and I was able to learn quite a bit here.