Sign problems with vectors, how can we "resolve" this....

[etotheipi]

There are a few details, either convention or understanding, that I was hoping someone could help to clarify. Consider the object below, acted upon by a few forces including an unknown $\vec{N}$, which I have split into its horizontal and vertical components $\vec{N_{x}}$ and $\vec{N_{y}}$. Suppose also that $\vec{N}$ is at an acute angle $\theta$ to the horizontal.

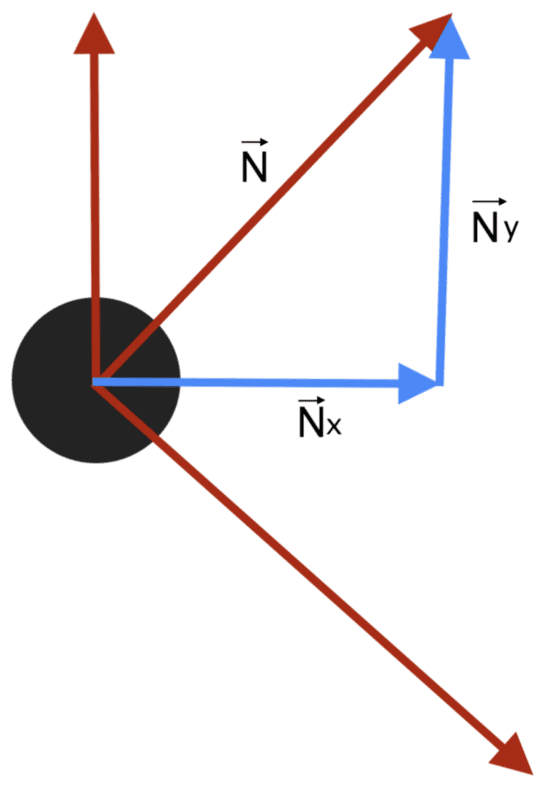
Geometry dictates that the magnitude of $\vec{N_{y}}$ is $|\vec{N}|\sin{\theta}$, and since it points in the defined positive $y$ direction we obtain $\vec{N_{y}} = (|\vec{N}|\sin{\theta})\vec{j}$. However, it is quite possible that if we were to solve the system by applying $\vec{F} = m\vec{a}$ horizontally and vertically, the vertical component of this normal force might come out to be negative. However, $|\vec{N}|\sin{\theta}$ can't be negative, so what gives?

My suspicion is that the problem has something to do with using $|\vec{N}|$ in the components of $\vec{N_{x}}$ and $\vec{N_{y}}$, but can't think of a reason as to why.

 

[jbriggs444]

However, $|\vec{N}|\sin{\theta}$ can't be negative, so what gives?

If $\theta$ is a negative angle (i.e. an angle in the fourth quadrant) then its sine is negative.

And indeed, if the y component is negative, an accurate drawing would show $\vec{N}$ in the fourth quadrant.

It is very often convenient to use signed angles in this manner.

 

[etotheipi]

If $\theta$ is a negative angle (i.e. an angle in the fourth quadrant) then its sine is negative.

And indeed, if the y component is negative, an accurate drawing would show $\vec{N}$ in the fourth quadrant.

It is very often convenient to use signed angles in this manner.

I see what you mean in this scenario, however suppose instead we have a system of of two particles which initially had a total momentum vector $\vec{p_{1}}$, then collided, and now have velocities $\vec{v_{1}}$ and $\vec{v_{2}}$. If we have no other information, we might draw both velocity vectors to the right so that e.g. $\vec{v_{1}} = |\vec{v_{1}}|\vec{i}$. Of course this is incomplete, since we might also have $\vec{v_{1}} = -|\vec{v_{1}}|\vec{i}$. However we have no way of knowing which is correct. What can we use in this case?

Or, if we altered the first situation slightly so that $\vec{N}$ points vertically upward, we would have $\vec{N_{y}} = |\vec{N}|\vec{j}$. This appears equally problematic.

 

[jbriggs444]

I see what you mean in this scenario, however suppose instead we have a system of of two particles which initially had a total momentum vector $\vec{p_{1}}$, then collided, and now have velocities $\vec{v_{1}}$ and $\vec{v_{2}}$. If we have no other information, we might draw both velocity vectors to the right so that e.g. $\vec{v_{1}} = |\vec{v_{1}}|\vec{i}$. Of course this is incomplete, since we might also have $\vec{v_{1}} = -|\vec{v_{1}}|\vec{i}$. However we have no way of knowing which is correct. What can we use in this case?

I do not see any advantage to insisting on non-negative scalars in this situation. Pick a sign convention and use signed scalars. Just write $\vec{v_1}=v_{1\text{x}}\ \hat{i}+v_{1\text{y}}\ \hat{j}$ and do not insist that $v_{1\text{x}}$ and $v_{1\text{y}}$ be non-negative.

There is no need to shift from one coordinate basis for vectors pointing to the northeast and a different coordinate basis for vectors pointing to the southwest. Use one coordinate system and save yourself the headache.

Note that the relevant definition of scalar does not require that they be positive. They are elements of an arbitrary field. [For typical purposes, they just have to be real numbers]

 

[Ibix]

I'd say your construction implies that $\vec N$ and $\vec n$ are parallel, not anti-parallel. Otherwise you'd have to allow for the possibility that $N=−|\vec N|$. If you don't know which way something is pointing you have to allow for the possibility that your chosen arrow is pointing the wrong way, and hence allow negative multipliers.

One way to think of it is to work in 1d. If I have 3 things and I want 2, how many things do I have to add? I presume you are comfortable with the idea of adding -1 thing, at least as a way of expressing the answer. In this case a "thing" is comparable to a basis vector and the -1 to your multiplier. (I think you actually need a continuous quantity rather than discrete "things" for the 1d case to be a proper vector space but, for these purposes, meh).

 

[jbriggs444]

This is sort of what I was thinking, however I am getting a bit muddled with the actual interpretation of these quantities.

For instance, if we return to the first scenario but make $\vec{N}$ point directly upward, suppose $N$ is the component (positive or negative) of $\vec{N}$ along the direction of the force arrow we have drawn (represented by unit vector $\vec{n}$; this gives $\vec{N} = N\vec{n}$.

Using lower case n for the unit vector does not seem like a very good choice here. It invites confusion.

Let us use unit vector $\hat{j}$. We decide that $\vec{N}$ just happens to line up so that it is parallel (or anti-parallel) with $\hat{j}$.

Now we want to be able to express $\vec{N}$ in coordinate notation, $(N_x,N_y)$ so that $\vec{N}=N_x \hat i + N_y \hat j$. We know that $N_x$ = 0. We just want to be figure out what to put in for $N_y$.

Simple: If $\vec{N}$ points upward (in the same direction as $\hat j$) then $N_y$ will be positive. If $\vec{N}$ points downward then $N_y$ will be negative.

There is no need to insist that $N_y$ has to be positive because of some imagined rule that "scalars are never negative". Magnitudes are never negative. Scalars can be.

Individual coordinate values are scalars, not magnitudes.

 

[Ibix]

Individual coordinate values are scalars, not magnitudes.

Indeed. $|\vec N|=\sqrt{N_x^2+N_y^2}$, which means that if $\vec N$ happens to be parallel to your y direction, $N_x=0$ and hence $|\vec N|=|N_y|$.

 

[jbriggs444]

I think you actually need a continuous quantity rather than discrete "things" for the 1d case to be a proper vector space but, for these purposes, meh.

Digression alert...

In a general vector space, the only requirement is that the scalars are a field. Some fields are discrete. For instance, the field with two elements (GF(2)) is perfectly valid to build a vector space with.

In one dimension, this would give rise to a vector space with two elements.

 

[etotheipi]

Now we want to be able to express $\vec{N}$ in coordinate notation, $(N_x,N_y)$ so that $\vec{N}=N_x \hat i + N_y \hat j$. We know that $N_x$ = 0. We just want to be figure out what to put in for $N_y$.

Right, so essentially whenever a vector has unknown parts it is best to define a new scalar component and work with that?

 

[jbriggs444]

Right, so essentially whenever a vector has unknown parts it is best to define a new scalar component and work with that?

Sure. You split the vector into components, write down an equation and solve for the value of the unknown component. The solution may come out positive or negative. In which case that coordinate will be positive or negative using the chosen coordinate system.

You choose the coordinate system when you split the vector into components. That includes specifying a sign convention. (right = positive, up = positive, etc).

 

[etotheipi]

Sure. You split the vector into components, write down an equation and solve for the value of the unknown component. The solution may come out positive or negative. In which case that coordinate will be positive or negative using the chosen coordinate system.

I thought I'd create a little problem to see if I'd got the hang of it - i.e. supposing the magnitudes of the tension, normal force and weight are known, as well as the direction of the tension, come up with some expressions for the frictional force at the wall.

Previously I would have written something along the lines of

$T\sin{(\theta)} + F - W = 0$
$N - T\cos{(\theta)} = 0$

and use this to solve the system. Evidently the frictional force must point upward by simple torque analysis, however supposing we didn't know this a positive or negative value for F would indicate so.

However, now I'd be inclined to say something like

$F_{y} \vec{j} + |\vec{T}|\sin{(\theta)} \vec{j} - |\vec{W}|\vec{j} = 0\vec{j}$
$|\vec{N}| \vec{i} - |\vec{T}| \cos{(\theta)} \vec{i} = 0\vec{i}$

This is a lot messier, but is it more accurate? I wonder what conventions more experienced physicists like yourself use?

 

[PeroK]

I would simply do this:

$T\sin{(\theta)} + F - W = 0$
$N - T\cos{(\theta)} = 0$

In general, I don't complicate things unless I have to.

 

[etotheipi]

I would simply do this:
In general, I don't complicate things unless I have to.

That's interesting; when you write $T$, $F$, $W$, what do you think of them as? I was in the habit of just calling them the force in a particular direction and calling it a day. However the letters could be inferred to mean either the magnitudes or the components of the vector?

 

[Ibix]

A real-world one - we are usually taught that for thin lenses $$\frac 1f=\frac 1u +\frac 1v$$In this case $u$ and $v$ are measured in opposite directions from the lens. But once you start chaining lenses together, the book keeping is easier if positive is always in the same direction. In that case, we define $$\frac 1f=\frac 1{l_2}-\frac 1{l_1}$$where $l_2$ is the lens/image distance (positive to the rear of the lens) and $l_1$ is the lens/object distance (also positive to the rear of the lens).

 

[PeroK]

That's interesting; when you write $T$, $F$, $W$, what do you think of them as? I was in the habit of just calling them the force in a particular direction and calling it a day. However the letters could be inferred to mean either the magnitudes or the components of the vector?

Perhaps I haven't analysed it that much. If the direction of all the forces is known, then I would put them in my FBD as magnitudes with an arrow to indicate the direction: $\rightarrow \ F$.

If the scenario gets more complicated, especially in something like EM, then I would tend to write things as proper vectors with all the relevant information: $\vec E = E\hat y$ (into page) and $\vec B = B \hat \phi$ (and I'd add an arrow to try to show the direction of $\hat \phi$).

I prefer $\hat x, \hat y, \hat z$ to $\hat i, \hat j, \hat k$, because that just seems like a waste of three letters that you might want to use for indices or the square root of $-1$.

 

[etotheipi]

I'll just summarise what's been clarified, if for nothing else a reference for me tomorrow...

• A vector of known direction can easily be split into components of known sign via geometry or otherwise
• If the direction of the vector is unknown, we can uniquely identify the vector using either placeholder scalar components (working in a particular basis), or a magnitude and an angle (which will self correct if in the wrong quadrant as @jbriggs444 mentioned)
• When working in a single dimension it's convenient to omit the basis vectors and work with just the algebraic components, unless the example gets complicated as @PeroK mentioned. It might also be worth noting that magnitudes and signed scalars shouldn't be confused, even though they are commonly written similarly for one dimensional motion.

 

[etotheipi]

In general, I don't complicate things unless I have to.

I've been thinking about it a little more and there's something that's bugging me a bit. Pretty much all of the mechanics I've done up until now has been in terms of signed scalars, i.e. negative velocities etc., however these appear to just be the components, which seem incomplete without the unit vector.

Whilst I can understand that

$a\hat{x} = \frac{d}{dt} v \hat{x}$ doesn't look as nice as $a = \frac{d}{dt} v$

it just seems strange to leave out the unit vectors. I.e. the velocity can't be negative, but it's components can. Perhaps the solution is to try to interpret any instance of e.g. $v$ as the component of $\vec{v}$ in a given basis instead. I have the feeling this might cause a bit of headache going forward!

 

[PeroK]

I've been thinking about it a little more and there's something that's bugging me a bit. Pretty much all of the mechanics I've done up until now has been in terms of signed scalars, i.e. negative velocities etc., however these appear to just be the components, which seem incomplete without the unit vector.

Whilst I can understand that

$a\hat{x} = \frac{d}{dt} v \hat{x}$ doesn't look as nice as $a = \frac{d}{dt} v$

it just seems strange to leave out the unit vectors. I.e. the velocity can't be negative, but it's components can. Perhaps the solution is to try to interpret any instance of e.g. $v$ as the component of $\vec{v}$ in a given basis instead. I have the feeling this might cause a bit of headache going forward!

A vector equation is really three equations:$$\vec F = m\vec a$$
is a shorthand for $$F_x = ma_x; \ F_y = ma_y; \ F_z = ma_z$$
I'm not sure that $a\hat{x} = \frac{d}{dt} v \hat{x}$ makes a lot of sense. What are $a$ and $v$?

Kinematics in one dimension can be seen as a special case where there is no motion in two of the directions, so you are left with a single equation for one component. Which you don't even have to label. So, in simple terms $$F = ma$$

 

[jbriggs444]

the velocity can't be negative

It can't be positive either. It is a vector.

It is somewhere between a useful shortcut and an abuse to view velocities as positive or negative in the one dimensional case.

 

[etotheipi]

A vector equation is really three equations:$$\vec F = m\vec a$$
is a shorthand for $$F_x = ma_x; \ F_y = ma_y; \ F_z = ma_z$$

But in the case $F_x = ma_x$, isn't $F_x$ the component of the one dimensional vector $\vec{F_x}$ and $a_x$ the component of $\vec{a_x}$? Or am I going bananas...

 

[PeroK]

But in the case $F_x = ma_x$, isn't $F_x$ the component of the one dimensional vector $\vec{F_x}$ and $a_x$ the component of $\vec{a_x}$? Or am I going bananas...

I'm not sure it helps in physics to think of one dimensional vectors, because there is nothing to be gained. You need two dimensions before it becomes worthwhile.

 

[etotheipi]

I'm not sure it helps in physics to think of one dimensional vectors, because there is nothing to be gained. You need two dimensions before it becomes worthwhile.

So if I wrote (in one dimension) $v = -3$, how would we interpret $v$ (perhaps just $\frac{dx}{dt}$?). I thought it was done something like $\vec{v} = v\hat{i} = -3\hat{i}$, however I can see why you say this isn't adding anything to understanding. It does however give $v$ an interpretation as the component of $\vec{v}$.

 

[jbriggs444]

But in the case $F_x = ma_x$, isn't $F_x$ the component of the one dimensional vector $\vec{F_x}$ and $a_x$ the component of $\vec{a_x}$? Or am I going bananas...

It does not matter greatly whether $F_x$ denotes the real-valued coefficient from the $(F_x,F_y,F_z)$ coordinate tuple that represents $\vec{F}$ or whether it denotes the vector-valued projection of $\vec{F}$ onto the x axis.

In the one case you can write $$F_x=ma_x$$ and the multiplication is multiplication of a real by a real.

In the other case you can write $$\vec{F_x}=m\vec{a_x}$$ and the multiplication is the multiplication of a vector by a scalar.

Since we are working in $\mathbb{R}^n$, the underlying operation is real multiplication either way. Don't sweat the small stuff.

 

[etotheipi]

I understand your point, but then the definitions appear to contradict and the logic starts to become circular. If I start building up the picture in one dimension, I let

$F_{x} = ma_{x}$

I can make both $F_{x}$ and $a_{x}$ negative, according to my sign convention. In one dimension, if this is all there is to go off, I don't see why we can have no negative acceleration. It would just mean that the rate of change of the rate of change of the $x$ coordinate is less than zero.

I make three copies of this equation for all three orthogonal directions, and I package all of them into a nice vector format. Of course, a vector has no sign, it's a different kind of object to a standard scalar. Now we would call $a_{x}$ a component, which we still allow to take on either sign.

But then is $a_{x}$ or $\vec{a}$ the acceleration? In nearly every introductory mechanics text, significant time is devoted to declaring that acceleration is a vector quantity, but they then proceed to use the scalar versions, i.e. just working in $\mathbb{R}$.

Thanks for your patience, I really appreciate it!

 

[jbriggs444]

I don't see why we can have no negative acceleration

What definition leads you to believe that there can be no negative acceleration?

 

[etotheipi]

What definition leads you to believe that there can be no negative acceleration?

If we take acceleration to mean the vector, as was mentioned earlier, a vector is neither positive nor negative. However the component of acceleration in one dimension can be negative. When working in one dimension, this component is apparently also called the acceleration. So I'm not sure which definition is definitive.

 

[jbriggs444]

If we take acceleration to mean the vector, as was mentioned earlier, a vector is neither positive nor negative. However the component of acceleration in one dimension can be negative. When working in one dimension, this component is apparently also called the acceleration. So I'm not sure which definition is definitive.

Why does it matter whether you say that it has a sign or you say that it does not?

If you want to do arithmetic with vectors you are going to write down a number for a coordinate value and perform arithmetic on the number. The number has a sign. That is all you need care about.

You can do algebra without caring whether an entity is positive, negative or neither. It's just a variable name.

 

[etotheipi]

is a shorthand for $$F_x = ma_x; \ F_y = ma_y; \ F_z = ma_z$$

Ah, I think I understand. Before we get into the vector structure, $F$ and $a$ etc. are scalars, literally just operating under the notion that a positive value of force produces a positive value of $\frac{d^{2}x}{dt^{2}}$ of our particle along the $x$ axis. Once we introduce the vector object, these scalars just become the components and contribute to the overall machinery.

A major source of the confusion appears to come from many texts stating the ability of a quantity like $a$ to take on negative values makes it a vector in itself, whilst it surely does not - a vector being a completely separate mathematical construction.

Of course, a one dimensional vector $\vec{a} = a\hat{x}$ is the alternative.

Is this what you were getting at?

 

[jbriggs444]

many texts stating the ability of a quantity like aaa to take on negative values makes it a vector in itself

You will need to provide a specific reference for us to know whether this is an incorrect source or an incorrect understanding of that source. The ability of a quantity to take on negative values does not make it a vector. For instance, an integer can be negative, but the set of all signed integers is not a field and is not a vector space. [i.e. is not a one dimensional vector space over itself under the usual rules for addition, subtraction, multiplication and division]

What makes something a vector is that it adheres to the rules for an element of a vector space.

As a practical matter, the numbers you most often encounter, the rational numbers and the real numbers, do meet the requirements to be one dimensional vector spaces. Further, the subset of non-negative rationals and the subset of non-negative reals do not meet those requirements. So the source(s) you are reading may not be completely out to lunch.

 

[PeroK]

Ah, I think I understand. Before we get into the vector structure, $F$ and $a$ etc. are scalars, literally just operating under the notion that a positive value of force produces a positive value of $\frac{d^{2}x}{dt^{2}}$ of our particle along the $x$ axis. Once we introduce the vector object, these scalars just become the components and contribute to the overall machinery.

This business of positive and negative values is not the issue. In terms of the physics, you start with the concept that a vector has, in some physical sense, a direction. In classical physics, that means a direction in 3D space. Mathematically this is called a directed line segment. In that sense, a vector is defined by a directed line segment.

Mass, charge, temperature, kinetic energy are not defined by a directed line segment. These are not vector quantities.

Position, velocity, acceleration, force, electric field can be defined by a directed line segment.

You can represent a vector in many ways. But, in general, you need three numbers to do this. You can use a Cartesian, spherical (polar) or other coordinate system.

Note that if you put the mass, charge and kinetic energy of a particle into an array this does not make it a vector. It is just three numbers with no underlying directed line segment. This is very different from the three components of a vector, which represent a directed line segment by an array of three numbers.

In fact, as you continue your studies you will find that the concept of which sets of numbers form a vector and which don't becomes more important.

 

[etotheipi]

This business of positive and negative values is not the issue. In terms of the physics, you start with the concept that a vector has, in some physical sense, a direction. In classical physics, that means a direction in 3D space. Mathematically this is called a directed line segment. In that sense, a vector is defined by a directed line segment.

Right, though in that case even for one dimensional motion we'd require $\vec{F} = m\vec{a}$, where $\vec{F} = F\hat{x}$ and $\vec{a} = a\hat{x}$. First we need to get all of our forces in terms of $\hat{x}$, which essentially defines the positive direction along the chosen axis.

I suppose then you could "cancel" $\hat{x}$ and end up with an equation containing $F$ and $a$. And by playing around for a little bit (proof by a few examples... my favourite method), I think it's the case that anyone dimensional situation can be described completely in terms of the components. Same goes for rotational dynamics; I don't often write $\theta \hat{z} = \omega t \hat{z}$, but just use the component terms.

In this vein, I don't think it makes sense to simply state $F_{x} = ma_{x}$ on its own without 'obtaining it' from the above sort of logic. Otherwise, the two quantities are completely undefined - the components cannot exist without the force vector!

 

[Mister T]

Once we introduce the vector object, these scalars just become the components and contribute to the overall machinery.

No, they were components all along. It's just that it's usually not made explicitly clear in the interest of brevity.

For example, the equation $v=v_o+at$ that is used in the study of one-dimensional motion should be written, for example, as $v_x=v_{ox}+a_xt$ to make it explicitly clear that we are talking about vector components and not vector magnitudes. Of course, that introduces an extra layer of complexity for students who are already struggling to understand things.

 

[etotheipi]

No, they were components all along. It's just that it's usually not made explicitly clear in the interest of brevity.

For example, the equation $v=v_o+at$ that is used in the study of one-dimensional motion should be written, for example, as $v_x=v_{ox}+a_xt$ to make it explicitly clear that we are talking about vector components and not vector magnitudes. Of course, that introduces an extra layer of complexity for students who are already struggling to understand things.

Yeah, I now realize that I was completely bluffing it in that post, now that I re-read it it's a little embarrassing.

Your post makes it clear

 

[robphy]

I think a big part of the problem is notation... and possible confusions when generalizing to high dimensions.

Right, though in that case even for one dimensional motion we'd require $\vec{F} = m\vec{a}$, where $\vec{F} = F\hat{x}$ and $\vec{a} = a\hat{x}$.

The more correct expressions [and less ambiguous expressions] are
$\vec{F} = F_x\hat{x}$ and $\vec{a} = a_x\hat{x}$... (where $F_x \equiv \hat x\cdot \vec F$)
since $F$ (in the context of vectors) is the magnitude of $\vec F$.
If you want to use $F$, then you can write $\vec F = F \hat F$ (where $F\equiv\sqrt{ \vec F\cdot\vec F}$ and $\hat F\equiv \vec F/F$).
The physical law is $\vec F=m\vec a$.

In a coordinate system, its components are $F_x=m a_x$, $F_y=m a_y$, etc... (where $F_x=\vec F\cdot \hat x$, etc... ).
So, $\vec F=ma_x \hat x + m a_y \hat y + \cdots$
In one-dimensional problems, this becomes:
$\vec F=ma_x \hat x$, or in component form $F_x=ma_x$.

Usually, since books start out in 1-D, then generalize to higher dimensions,
this component equation $F_x=ma_x$ is
often written as $F=ma$ (for simplicity, since $F_x=ma_x$ is too complicated?),
where $F$ and $a$ are really signed $x$-components of force and acceleration,
although the phrase "signed $x$-components of" is usually omitted.

Then, generalizing to higher-dimensions,...
in many physics books, the convention is "a vector $\vec F$ with its arrowhead removed" or "a vector ${\bf F}$ unbolded",
$F$ represents the vector magnitude:
$F= | \vec F |= \sqrt{\vec F\cdot\vec F}$
or $F= | {\bf F} |= \sqrt{{\bf F}\cdot{\bf F}}$ .
So, $\vec F = F \hat F$...(for simplicity, because $\vec F = |\vec F| \hat F$ looks too complicated?)
but this "$F$" meaning "$|\vec F|$" (the non-negative magnitude) here
is different from "$F$" meaning "$F_x$" (the signed component along $\hat x$) in the previous paragraph.

So, there is now a clash in notation... since $F$ has been doing double-duty to avoid complication(?).

 

[etotheipi]

I think a big part of the problem is notation... and possible confusions when generalizing to high dimensions

The more correct expressions are ...

Wow, this is a great reference resource - retroactively helps me to understand a lot of what has already been said in the thread that I hadn’t totally gotten yet! Thanks!