Splitting Fields: Anderson and Feil, Theorem 45.6 ....

[Math Amateur]

I am reading Anderson and Feil - A First Course in Abstract Algebra.

I am currently focused on Ch. 45: The Splitting Field ... ...

I need some help with an aspect of the proof of Theorem 45.6 ...

Theorem 45.6 and its proof read as follows:

At the start of the proof of Theorem 45.6 we read the following:

"Suppose that $K$ is a normal extension of $F$, a field with characteristic zero. Then by Theorem 45.5, $K = F( \alpha )$, where $\alpha$ is algebraic over $F$. ... .. "
Can someone please explain exactly how $K = F( \alpha )$ follows in the above statement ... ?The quote mentions Anderson and Feil's Theorem 45.5 and also mentions that K is a normal extension so I am providing the statement of Theorem 45.5 and Anderson and Feil's definition of a normal extension as follows ... ...

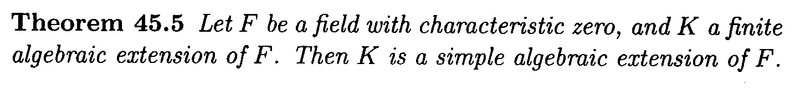
Hope someone can help ...

Peter

 

[fresh_42]

Gather what you have: $F \subseteq K$ a finite extension. This means $\dim_FK =: n < \infty$.
Now what does that mean for $\{1,a,a^2,a^3,\ldots ,a^n\}\,$, if we take an arbitrary element $a \in K\,$?
Can you deduce from that, that the conditions for Theorem 45.5 are met?
And what does $F \subseteq K$ simple algebraic extension mean?

 

[Math Amateur]

Thanks for the advice to "Gather what you have: ... "...

I was myopically focused on the first sentence of the proof where we are given

(i) $K$ is a normal extension of $F$
(ii) $F$ is a field with characteristic zero

and was wondering about how to get from this to the initial conditions of Theorem 45.5 that

(i) $F$ is a field with characteristic zero
(ii) $K$ was a finite algebraic extension of $F$ BUT ... in my tunnel vision I neglected that $K$ was given as a finite extension ... sorry for such a simple oversight ...... HOWEVER ... still concerned that we need to establish that $K$ is algebraic over $F$ ... that is all elements of $K$ are algebraic over $F$ ... before applying Theorem 45..5 ...Peter

 

[fresh_42]

... HOWEVER ... still concerned that we need to establish that KKK is algebraic over $F$ ... that is all elements of $K$ are algebraic over $F$ ... before applying Theorem 45..5 ...

That's why I wrote - with $n$ being the dimesion of $K$ over $F$

Now what does that mean for $\{1,a,a^2,a^3,\ldots ,a^n\}\,$, if we take an arbitrary element $a \in K\,$?

How many elements has this set? Can they be linear independent, and if not, what does that mean?

 

[Math Amateur]

Gather what you have: $F \subseteq K$ a finite extension. This means $\dim_FK =: n < \infty$.
Now what does that mean for $\{1,a,a^2,a^3,\ldots ,a^{ n - 1} \}\,$, if we take an arbitrary element $a \in K\,$?
Can you deduce from that, that the conditions for Theorem 45.5 are met?
And what does $F \subseteq K$ simple algebraic extension mean?

Just to answer your questions ...

You write:

"Now what does that mean for $\{1,a,a^2,a^3,\ldots ,a^n \},$, if we take an arbitrary element $a \in K\,$?"

It means that $\{1,a,a^2,a^3,\ldots ,a^{n - 1} \} ,$ is a basis for the vector space $K$ over $F$ ... and that $\{1,a,a^2,a^3,\ldots ,a^n \},$ is a linearly dependent set ... ... is that correct?

You write:

"Can you deduce from that, that the conditions for Theorem 45.5 are met?"

... regarding conditions for Theorem 45.5 to be met ... see my previous post ...
You write:

"And what does $F \subseteq K$ simple algebraic extension mean?""Means that $K$ is of the form $K = F( \alpha )$ ...

Peter

 

[Math Amateur]

That's why I wrote - with $n$ being the dimesion of $K$ over $F$

How many elements has this set? Can they be linear independent, and if not, what does that mean?

As mentioned in the previous post the set is linearly dependent ... so this means that any element of the set can be expressed as a linear combination of the others ...

Peter

 

[fresh_42]

It means that $\{1,a,a^2,a^3,\ldots ,a^{n - 1}\}$ is a basis for the vector space $K$ over $F$ ... is that correct?

I don't know. I don't care either. This would exclude e.g. all $a \in F \subseteq K$ without reason.

It means the set $\{1,a,a^2,a^3,\ldots ,a^{n}\}$ is linear dependent - in any case. Linear dependency means, we have a non trivial expression of zero: $0 = c_0\cdot 1 + c_1\cdot a + c_2\cdot a^2 + \ldots + c_n\cdot a^n$ with not all $F \ni c_i=0$. If we define $p(x)=c_0\cdot 1 + c_1\cdot x + c_2\cdot x^2 + \ldots + c_n\cdot x^n$ we get a polynomial in $F[x]$ with $p(a)=0$ and $a$ is algebraic.

$K=F(\alpha)$ for a certain $\alpha \in K$ is the result of theorem 45.5.

 

[Math Amateur]

Thanks for all your help fresh_42 ...

Gradually building a basic understanding of Galois theory, thanks to your support ...

Peter