- #1
Leo Liu
- 353
- 156
- Homework Statement
- Merry
- Relevant Equations
- Christmas
Question 7.6

Official solution
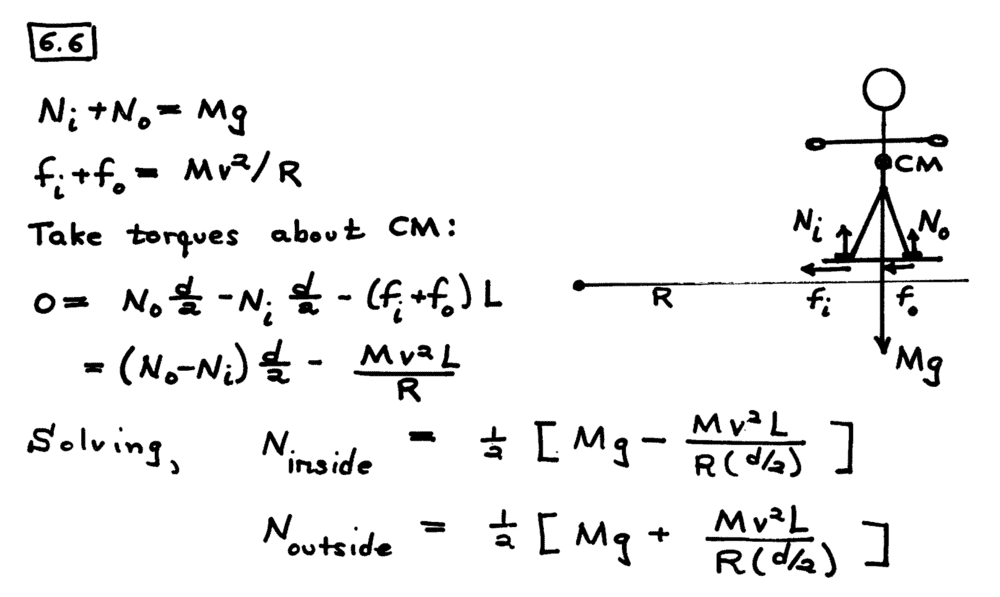
It seems that the solution uses the conservation of angular momentum to solve this question (τ=0). But the problem is that the frame is set on the centre of mass of the guy, which is non inertial. I would like to know why it is correct to do it this way. My guess is that the author implicitly uses the Konig theorem and measures L of the system at the fixed centre of the circle, and since the force is central, Ls of both CM and the system remain constant. Therefore, L measured at CM is constant ⟹ τ=0. Is my inference correct?
Happy holiday .
.
Official solution
It seems that the solution uses the conservation of angular momentum to solve this question (τ=0). But the problem is that the frame is set on the centre of mass of the guy, which is non inertial. I would like to know why it is correct to do it this way. My guess is that the author implicitly uses the Konig theorem and measures L of the system at the fixed centre of the circle, and since the force is central, Ls of both CM and the system remain constant. Therefore, L measured at CM is constant ⟹ τ=0. Is my inference correct?
Happy holiday
Last edited: