Gyroscope - I just don't get it.

[quasar987]

I don't understand why a rotating gyroscope whose rotation axis is inclined with respect to a vertical axis does not fall to the ground dues to gravity as fast as the non-rotating giroscope.

Thanks for your replies.

 

[Gonzolo]

Until a more elaborate answer comes along, consider that a red dot on the outer edge of the spinning mass wants to go as straight as possible, just like a red dot painted on a moving mass in free space. The red dot (the local mass it represents) has inertia, rotationnal inertia in this case, which tends to keep it going in the initial manner.

 

[quasar987]

Ok so could it be that the answer is: An ideal rotating giroscope will never fall to the ground due to gravity because it has a vertical component of angular momentum and since the gravitationnal force exerts no vertical (y) torque , the vertical component of angular momentum must be conserved. So the thing will rotate about the vertical axis due to the components of gravitationnal torque in the x-z plane but will not fall to the ground because that would mean losing vertical angular momentum.

On the other hand, the non-rotating gyroscope having no angular momentum at all will fall to the ground WHILE gaining a little bit of angular momentum in the x-z plane because of the gravitationnal torque being exerted for the time of the fall.

 

[notsureanymore]

I came to this forum for exactly the same question. quasars last note is confusing at best.

A spinning gyroscope overcomes gravity, How?

"rotating gyroscope whose rotation axis is inclined with respect to a vertical axis"

consider only two directions UP and DOWN.

The VERTICAL spinning top attempts to "throw" itself in all directions on the plane os spin (horizontal). Because these forces are balanced it is stable and does not fall.

But when inclined on an angle we introduce another force "gravity", which increases the downward force generated by the top, and reduces the upward force generated by the top

The top is now out of balance and **should** come crashing down to earth.

But it does not ? Why not.

(laymans terms please, I am smart enough but have never done higher levels of math)

Chris.

 

[quasar987]

Too bad no one answered to my last note, I still don't know if that's the reason or not. If it is, then I still find the phenomenon peculiar. I'ts as if one law of physics (conservation of angular momentum) was "more important" or had priority over the other (gravity).

But when inclined on an angle we introduce another force "gravity", which increases the downward force generated by the top, and reduces the upward force generated by the top.

What are those forces generated by the top you talk about?

 

[notsureanymore]

Hi quasar.

The forces I speak of are in effect the red dot spoken of earlier.

Imagine a weight attached to the spinning top, when the top spins the weight attempts to pull the top in the weights current direction. in other words its out of balance pulling the top in the direction of the weight.

Without the weight the tops own mass is doing the same thing but in every direction at once, ie balanced. (only at 90 degrees to the spinning axis).

but on a top that is not perpendicular to gravity. the force created by the spinning top now MUST be out of balance. this you understand otherwise you would not have asked the original question.

Its as if the rotating force of the top 'ignores' the force of gravity

In fact if you attempt to change the angle at which the top is leaning the top will resist the change.

To feel that resistance pick up a barrel vacuum cleaner while it is running. it kicks and bucks in your hand if you attempt to move it into another plane.

Chris H.

Note:
The upward and downward only relate to the fact these forces are not parallel to the surface of the Earth (gravity) in an inclined top.

 

[DaveC426913]

A spinning top does *not* defy gravity.

You must support one end of the top, else it will fall to the ground just like every other object. If you put the supported end on a weigh scale, it will weigh exactly as much as if it weren't spinning at all.

So, the only mystery is why its *orientation* appears to defy gravity. (Spin the top and put its axis of revolution horizontal. Place one end of the spinning top on your finger. It looks like it should fall off your finger, but does not. That's the mystery.)

Consider a non-rotating top on your finger. If you try to support it with a finger under only one end, it will fall (obviously). But before it falls, it has to *rotate* slightly until its support "clears" your finger. Only then can it proceed to the ground.

The spinning top is merely resisting that tendency to rotate slightly. Since it won't rotate, it can't get its support off your finger. (But not that it still presses down on your finger with the same weight a non-spinning top does.)

 

[notsureanymore]

Ok
I assume you mean "the long axis of the top must rotate around your finger before falling"
given that assumption, for a top which is not rotating about its own axis gravity applies normally. and the top topples as one would expect.
(a more precise description would be something like it must rotate around its point of contact on the surface of your finger)

Then you go on to state

The spinning top is merely resisting that tendency to rotate slightly.

This is the crux of the matter, you pass it off with no explanation.

WHY does the top resist to rotate. even when it is already rotated off the vertical
A top spinning with its axis off the vertical will hold the angle of rotation until the top loses enough speed, then it topples. Why?

I have attached an image to further explain what my dilemma is

 

[Romperstomper]

Yea, i just "seems" to defy gravity, but it doesn't. Using a top as an example: Take a top that's not spining and mark a spot on the outer edge of it. If you tilt the top slightly towards spot, there will be more downward force on that part of the top so it will start to tilt and fall that direction. Rotate the top 90 degrees. Where the spot is on the top no longer has that downward force, but it still has the veocity from it so the top will lean towards the new position of the spot. Rotate it another 90 degrees and the same thing happens. Keep doing it over and over again and eventually the top will be leaning towards that new direction. Keep going and it will be leaning in the opposite direction of the initial tilt you gave it. So, the top will just wobbles instead of falling over.

That's the best explanation I can come up with.

 

[notsureanymore]

I'll try again with the attachments
broken into two due to size

 

[notsureanymore]

Hi Romper take a look at the images, (shame they didnt show) you will see what I mean

your explanation works perfectly for a top with a vertical axis. its the off vertical that is of greatest concern

 

[notsureanymore]

P.S. By inclining the top we are moving its centre of gravity until it is no longer directly above the point of contact on the surface. the centre of gravity is now suspended, without support. yet it behaves as if it is unmoved.

I would like to experiment but don't have the nec. equipment
exp. 1. spin top in vertical position. weigh it
exp. 2. spin top in inclined position. weigh it

Are they the same? if so why?, if not why?

Where is the centre of grav for both of the above? the centre of mass or the point of contact with the surface.

Has the centre of gravity moved down the top to the point of contact. thus no topple?

 

[Romperstomper]

Actually, I think my explinations is flawed. Gyroscopes don't rotate that direction, they rotate in the opposite direction of spin. The way they work is shown in your second drawing.

If the axis is tilted and the gyroscope is spinning, then the upward force on one side will hold that side up, while the extra downard force on the other will make the gyroscope fall towards that side. This is exactly why tops wobble, because its axis does start to move out of the vertical position. If it didn't, then precession would never occur.

 

[notsureanymore]

I just had an interesting thought. Is gravity 'sticky'

What I mean by this is gravity attaches itself to the downward spin of the gyroscope. and the gyroscope is thrust toward the floor.

Now the spin of the gyroscope causes that gravity particle (stay with me here) which has attached itself to the down side, is now being thrown upwards.

This upward moving gravity particle is now opposite the new downward particle which attached itself to the now downward side of the top these two gravity particles cancel each other out thus the overall effect of gravity is nil.

:-)

Of course I see many flaws in this argument. but the idea of sticky gravity is interesting. at least in that it has momentum and its direction can be changed.

Hey its no weirder than 11 dimensions!

 

[cepheid]

This is very hard to explain without diagrams, but I don't think the fanciful explanations we're getting ourselves into are really necessary. Consider an analogue in translational motion first:

A ball on a string, at rest, will accelerate toward you if you grab the end of the string and pull on it, making it taut.

Now, what about a ball with some initial translational momentum? You pull on the string in a direction perpendicular to the ball's initial velocity, and voila! It suddenly begins to move in a circular loop about your hand. But it's distance from your hand does not change! You are pulling it toward you...why is it not responding as in the first case? Is it defying the tension force? Obviously not...we know that the tension force acts as a centripetal force. A simple analysis of the vectors reveals why the object with some initial translational momentum "behaves" differently under some applied force than an object at rest.

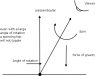
The same is true in the rotational case. Consider a rotating bicycle wheel. with a string attache to the centre. When it has no angular momentum (it is not spinning), and you try to hold in in the vertical orientation, it will fall back down:


|
| <--- string
|
| / <--- wheel
/

side view of the wheel, hanging from a string, almost vertical. Why does it flop back down? In the position shown above, the centre of mass is no longer directly below the pivot point (where the string is attached), so the gravitational force exerts a torque that rotates the wheel back down to this position:

_______|
_______| <----string
_______|
_______|
_____------ <---- wheel

Now, what happens when the wheel is spinning (ie it has some inital angular momentum pointing roughly to the right, for example. The very same torque (which points into the page), has a very different effect...that angular momentum vector does not decrease (because the torque is perp. to it), and it changes direction...so the wheel remains vertical even after you let go! But it precesses (rotates about an axis // to the string in this case):

|
| <--- string
|
| / <--- wheel (now spinning, so it remains in this orientation)
/

So, in a direct analogy to the previous example, an object with some initial angular momentum reacts differently (and in a non-intuitive way) to an applied torque than an object initally non-rotating does. For those of you (probably everyone) who couldn't make heads or tails of my stupid diagrams, please check out the video here, and read the article...it explains gyroscopes quite well:

http://science.howstuffworks.com/gyroscope1.htm

 

[DaveC426913]

I'll try again with the attachments
broken into two due to size

I have never seen math like this. Gravity does not attach itself to other forces. Gravity acts on the object as a whole.

 

[DaveC426913]

P.S. By inclining the top we are moving its centre of gravity until it is no longer directly above the point of contact on the surface. the centre of gravity is now suspended, without support. yet it behaves as if it is unmoved.

(Centre of gravity? You mean centre of mass.)

The centre of mass has support. It is supported by the rigid metal structure of the top. One end of the top is resting on my finger.


Look, I'm not suggesting it is inherently stable in that position, I'm merely trying to get you to realize that gravity is not the force to worry about here. There is no doubt why the object doesn't fall due to gravity, the big question is, why does the object resist rotation.

I would like to experiment but don't have the nec. equipment
exp. 1. spin top in vertical position. weigh it
exp. 2. spin top in inclined position. weigh it
Are they the same? if so why?, if not why?

They will weigh the same. I'll bet 10 million dollars on it. Or to put it another way, if you manage to use a gyroscope to reduce the mass of an object, I'll raise and give you all the money you need, since you will have revolutionized technology. (Imagine jumbo jets, powered by gyros, weighing nothing at all).

 

[Romperstomper]

Hmm, I just re-read my second post and it doens't make much sense. My first explanation looks right. I guess that's what happens when I get too tired, heh. Thanks for the explanation Cepheid.

 

[BobG]

DaveC426913 is giving you the correct description of what is happening. It's not that gravity isn't still pulling down the same as it always was. The gyroscope isn't resisting gravity anymore than a block sitting on a table is resisting gravity's urge to pull it to the floor.

Gravity is a weak force (just keep telling yourself that all the way down the side of the cliff). You can resist it with a pretty small magnet. But the force of gravity has to have some effect on the gyroscope.

It still creates a torque that tries to rotate the gyro off the string, but it can't overcome the angular momentum of the gyro. It will cause the gyro to precess around the string.

This has some good info on gyros and how they work. I started at the top of the gyro section, but the specific info you want is buried down a few different branches.
http://hyperphysics.phy-astr.gsu.edu/hbase/gyr.html

 

[notsureanymore]

This is very hard to explain without diagrams, ...
so the wheel remains vertical even after you let go! But it precesses (rotates about an axis // to the string in this case):

...

please check out the video here, and read the article...it explains gyroscopes quite well:

http://science.howstuffworks.com/gyroscope1.htm

Excellent so now I understand what precession means. I couldn't pick it up from my reading of the dictionary.

I always thought the reason the top rotated around its pivot was simply due to the friction of the pivot on its support. I did not realize that this was precession. that's why it was not shown in my drawings its the missing 'force' that counter balances the WEAK force of gravity.

DaveC426913wrote...

(Centre of gravity? You mean centre of mass)

aren't the two synonymous? it was always called the centre of gravity to me.

Now I know this is going to sound STUPID! it does to me now, but when I spoke of sticky gravity. (oh god I feel stupid admitting this). I was talking about inertia. but in my infantile way I called it sticky gravity if I had thought with a reasonable number of synapses instead of the few I put on it somewhat jokingly, I would have realized that for every section of the top it develops Inertia. that Inertia is then displaced as the wheel rotates and its is now acting in a slightly different direction.

This happens continously as the top rotates, and you have precession.

Thats what I meant by the momentum of gravity can change direction. (stupid description, I apologise to those with sensitive minds)

momentum of gravity = inertia.

Ok I fully understand why a gyroscope does not fall.

Thanks to all for this wonderful exercise of discovery.

P.S. DaveC I'd love to take the money off you. but can it wait for my next extraordinary Gaff

 

[Schneibster]

Nice and easy. We'll start out with a gyroscope with its axis pointing straight out. That's the most interesting way, after all. They usually come with a little stand that you can put one end of the frame on; as long as it's spinning, it will stick straight out from the stand, appearing to defy gravity. So imagine that the axis is pointing right at you, and the wheel is spinning clockwise.

Let's start with a bit of matter that's up at the top of the wheel. First of all, it's held within the wheel, which is solid, and the wheel is going around, so it wants to go around. But while its going around, gravity is pulling at it- and that makes it want to fall. So what happens is a combination of those two things: it spins, and it falls a bit too. But by the time it's gotten further down, that falling isn't making it go straight in toward the axis any more; now it's just kind of at an angle. If the whole gyroscope were to move so that it was pointing at your left arm instead of the middle of your chest (or your nose, whatever), then both of those things could happen. So it does; and if you have a real gyroscope, spinning just the way I've described, you'll see it does. Not only that, but it keeps on turning around that way; it's called "precession." The interesting thing about precession is that the Earth does it, too! Only really slowly; it takes about 26 thousand years. That's longer than the time since the last ice age.

In other words, instead of making the gyroscope fall, the gravity made it go off at a right angle. This is a general principle; if you stand the gyroscope up so it's pointing straight up, and push away from you on the top, it will try to go right (assuming it's turning clockwise when you look down on it). That's why, when you hold it in your hand, it feels so weird and squirrely; it's trying to move always at a right angle to where it's being pushed.

 

[notsureanymore]

Let's start with a bit of matter that's up at the top of the wheel. First of all, it's held within the wheel, which is solid, and the wheel is going around, so it wants to go around.

Since when?

I thought it wants to go straight.
Just like any other mass when shoved. (inertia)

Trouble is it can't 'cause its attached to the top and every other part of the top wants to go straight as well but all in different directions.

So instead they vote and settle on an ammicable arrangement which is to go round. (the hand of god err the string puller decides the direction)

But should a small chunk break off it will go back to its original wish and go straight (well at a tangent)

A larger chunk breaking off will try to go straight as well, but it can't because the smaller chunks inside it want to go straight. Just in different directions. so the large chunk CURVES away from the top.

NOW

STEP this up to planetary scales and the large chunk may be effected by the mass of the top in such that it tries to curve away but when the outward force matches the force of the mass of the top (gravity) it can't go any further.

Then it is said to be in orbit and we call it a moon.

 

[notsureanymore]

STEP this up to planetary scales and the large chunk may be effected by the mass of the top in such that it tries to curve away but when the outward force matches the force of the mass of the top (gravity) it can't go any further.

Theres a problem with this, can anyone see what it is ?

 

[reilly]

Most freshman physics books will tell you what you need to know. The basic idea, for a tilted spinning top with a fixed point at the bottom, the torque generated by gravity is perpendicular to the vertical axis through the fixed point, and to the lever arm , itself perpendicular to the vertical axis. Thus the torque generates a rotational motion about the vertical axis. All of this stems from the properties of vector or cross products of vectors. (Not too different from the magnetic field from a long straight current.)

Regards,
Reilly Atkinson

 

[DirtyDan]

I understand why a gyroscope would resist rotation, since it would change its net inertia and such. But, if a gyroscope is on a tilted axis, would we agree that it has to spin faster in order to stay upright than it would if it was balanced? After all, if you truly were able to "balance" a gyroscope on its center, it could stay upright without spinning. This is impossible on a rotated axis, its is not resting over its center of (mass, gravity? center of mass is a new concept to me, heh)

 

[PBRMEASAP]

I think the basic idea behind the precession of a gyroscope can be understood without explicitly doing any detailed vector algebra (although that makes the reasoning a lot easier). All you have to accept are three things:

1) Angular momentum is a vector quantity: as such, it can be resolved into components along the three axes.

2) Much like ordinary momentum, the individual components of angular momentum are conserved in the absence of a corresponding component of torque. In particular, the total angular momentum vector (direction and magnitude) is conserved in the absence of any torque.

3) Two vectors can be added tail-to-head to form a resultant vector. Since angular momentum behaves like a vector, the total angular momentum vector is obtained by adding the three component angular momentum vectors tail to head in any order.

It is difficult to picture the argument that follows without some visual aid, so if you have a toy gyroscope, break it out!

As suggested in an earlier post, the best way to picture what's happening is to imagine resting the base of the gyro on something (a loop of string maybe) and steadily holding the top of the gyro out horizontally with your fingers. Since your fingers balance the force (and therefore torque) caused by gravity, the gyro's total angular momentum is conserved--it keeps on spinning and does not try to wiggle out of your hands. At this point, the total angular momentum vector is in the horizontal plane along the axis of the gyro. At the moment you let it go, gyro does exactly what you think it would--the top of the gyro starts moving toward the ground (the base is still supported by the loop of string). But this can't continue for more than an instant. If it did, the gyro would be angled slightly downward, and so would the total angular momentum vector. That is, the total angular momentum vector would have a slight downward vertical component--but this can't be the case. To see why, note that vertical force of gravity produced a torque in the horizontal plane, and this was the only unbalanced torque acting on the gyro. That means gravity can only affect the horizontal component of the angular momentum (by (2) above) . But since we set the gyro up so that its vertical component of angular momentum was zero, it must stay zero. Here's how the gyro resolves this problem. When the gyro starts falling, it simultaneously starts to rotate in the horizontal plane to produce an upward vertical component of angular momentum that exactly cancels the downward component. This net rotation is the precession that you observe.

That is the basic idea with precession. It is the gyro's way of conserving the vertical component of angular momentum.

That being said, that was far from being the whole story. Rigid body rotation is a very complicated thing--don't let anyone fool you. It turns out that the initial "downhill" motion I described generates a so-called "inertial" force that acts on the massive part of the gyro. This force acts at 90 degrees to the instantaneous linear velocity of the gyro's center-of-mass. This is the very same force that acts on a spinning figure skater's arms when she draws them into speed up her rotation. Working together with gravity, they cause the gyro to "climb the hill" again until the gyro is again horizontal but displaced slightly from where it was. This motion repeats over and over very quickly, so that the top of the gyro traces out an upside down cycloid. The up-and-down wobble motion is called "nutation." Often the amplitude of the nutation is so small that you can't see it--the gyro appears to be precessing steadily with no wobbles.

I'm not sure which is easier: following this argument or just sucking it up and learning vector mechanics. This is why math is so convenient. But I think it is also good to take a step back once in a while and see if you really understand what your math is telling you. However, an attempt to analyze fully the motion of a gyroscope in words would prove to be an embarrassment for most people, including myself.

 

[notsureanymore]

I did the bicycle wheel trick. and attached a bike wheel to a rope suspended from the ceiling.

It was quite fascinating to try and force the spinning wheel down by grabbing the unsuspended axle and pushing it down toward the floor. the more you pushed the more it resisted.

Another interesting test was to grab the axle and try to prevented it from precessing. the net result was the wheel tried to rotate around my hand. again with a stronger force than one would expect. Spin rate and the mass of the wheel of course would effect this strength.

 

[Creator]

...

Another interesting test was to grab the axle and try to prevented it from precessing. the net result was the wheel tried to rotate around my hand. again with a stronger force than one would expect. Spin rate and the mass of the wheel of course would effect this strength.

That reminds me of a somewhat infamous fellow who presented this interesting result to (I believe) the Royal Society.

Do as you have done with the bicycle wheel, spinning it up fast, but this time when it begins to precess twist your hand around so it tries to move upward (against gravity) and as it does raise your hand with it so the entire assembly goes over your head. It should cooperate with you relatively easily in getting it above your head.
Now stop the spinning, and again grabbing it by the axis with one hand, raise the wheel above your head and hold it there.
Which way is easier do; IOW, which is the harder way to get it above your head? Is it hevaier when spinning or heavier when stationary?

Creator

--Honk if you like peace and quiet--

 

[notsureanymore]

Its easier to simply grab the rope and try and lift it.

net result - it weighs the same either way. which in itself is a problem (to me)

The force that causes the precession acting at right angles to the rotation of the wheel, is also working to try to make the wheel fall to earth.
The rope is of course preventing that.

BUT as the wheel rotates why doesn't that inertia move to the top and try and make the wheel rise against gravity. (imagine the little red dots every one likes so much)
Its the same force that causes the wheel to start to topple and therefore starts the precession process, as is trying to make the wheel drop.

To get a visual idea draw a red arrow at the top and bottom of the wheel pointing down. now rotate the wheel 180 degrees those arrows are pointing up and the resulting movement (inertia) is also 'going' up.

If you cut the supporting rope shouldn't the wheel just hover in mid air?

 

[notsureanymore]

Creator, I re read your post. My response about lifting the rope was inadequate

As the spinning wheel precesses around your hand it moves into a horizontal position and you can lift it easily, but if the wheel is not spinning you must lift its weight which is unchanged AND twist the wheel into the horizontal position. the force on your wrist due to the very small leverage provided by the axle stub would in my opinion make it appear as though the wheel weighed a lot more.

Is this what you are getting at?