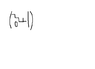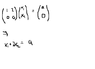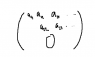aaaa202
- 1,144
- 2
How come the rank of a matrix is equal to the amount of pivot points in the reduced row echelon form? My book denotes this a trivial point, but unfortunately I don't see it :(