yungman
- 5,741
- 294
I have to thinking about how the skin effect come into play in transmission lines with two conductors and dielectric in the middle.
For normal skin effect, we consider a potential across a conductor as shown:
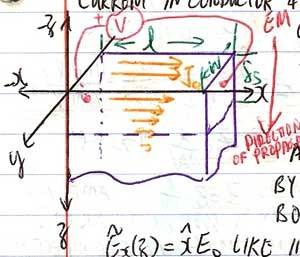
Where the tangential E right above and right below the surface at z=0, are equal. The E will cause J0 to flow as show in orange arrows. The J decrease as it goes deeper into the +z direction as E attenuates with depth.
But for a parallel plate transmission line as shown:
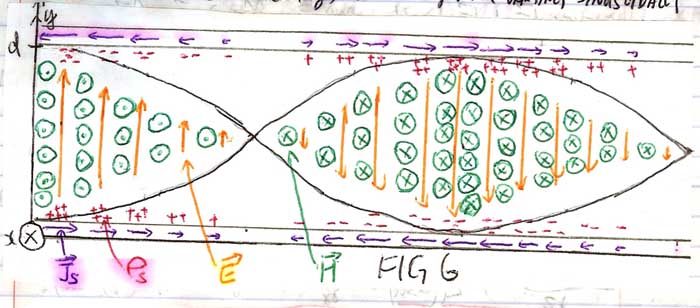
As TEM wave travel from left to right, E is in y direction and H in x direction. Boundary condition produce Js as shown in purple color at the surface of the conductors by H, and ρ in red from E.
We know we need to consider skin effect in the two plates. How do I calculate the skin effect? The E is normal to the surface of the conductor, but current flow is parallel to the conductor plates. I have no question the E attenuate as it penetrates normal to the conductor plates, BUT the current flow is parallel to the plates.
Please help me understand this.
Thanks
For normal skin effect, we consider a potential across a conductor as shown:
Where the tangential E right above and right below the surface at z=0, are equal. The E will cause J0 to flow as show in orange arrows. The J decrease as it goes deeper into the +z direction as E attenuates with depth.
But for a parallel plate transmission line as shown:
As TEM wave travel from left to right, E is in y direction and H in x direction. Boundary condition produce Js as shown in purple color at the surface of the conductors by H, and ρ in red from E.
We know we need to consider skin effect in the two plates. How do I calculate the skin effect? The E is normal to the surface of the conductor, but current flow is parallel to the conductor plates. I have no question the E attenuate as it penetrates normal to the conductor plates, BUT the current flow is parallel to the plates.
Please help me understand this.
Thanks